
分析 根据a+b+c=1得出a+b-c=1-2c,b+c-a=1-2a,c+a-b=1-2b,即将已知等式的分母进行变形,把式子$\frac{1}{a+b-c}$+$\frac{1}{b+c-a}$+$\frac{1}{c+a-b}$=1,通分后,去分母,把a+b+c=1整体代入即可得出结论.
解答 解:∵a+b+c=1,
∴a+b-c=1-2c,b+c-a=1-2a,c+a-b=1-2b,
∴$\frac{1}{a+b-c}$+$\frac{1}{b+c-a}$+$\frac{1}{c+a-b}$,
=$\frac{1}{1-2c}$+$\frac{1}{1-2a}$+$\frac{1}{1-2b}$,
=$\frac{(1-2a)(1-2b)+(1-2c)(1-2b)+(1-2a)(1-2c)}{(1-2a)(1-2b)(1-2c)}$,
=$\frac{3-4(a+b+c)+4(ab+ac+bc)}{(1-2b-2a+4ab)(1-2c)}$,
=$\frac{3-4+4(ab+ac+bc)}{1-2(a+b+c)+4(ab+ac+bc)-8abc}$,
∵$\frac{1}{a+b-c}$+$\frac{1}{b+c-a}$+$\frac{1}{c+a-b}$=1,
∴-1+4(ab+ac+bc)=-1+4(ab+ac+bc)-8abc,
∴8abc=0,
∴abc=0,
故答案为:0.
点评 本题是分式的加减法运算,灵活运用分式的加减法和整体代入的方法将所给的分式进行化简;异分母的分式相加减时,要化成同分母分式,先通分,化成同分母分式后,分母不变,分子相加减,按此法则进行计算可以得出abc的值.


科目:初中数学 来源: 题型:选择题
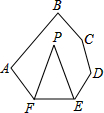 如图,在六边形ABCDEF中,∠A+∠B+∠C+∠D=460°,FP、EP分别平分∠AFE,∠FED,则∠P的度数是( )
如图,在六边形ABCDEF中,∠A+∠B+∠C+∠D=460°,FP、EP分别平分∠AFE,∠FED,则∠P的度数是( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com