
【题目】如图,已知在矩形ABCD中,M是AD边的中点,BM与AC垂直,交直线AC于点N,连接DN,则下列四个结论中:①CN=2AN;②DN=DC;③tan∠CAD=![]() ;④△AMN∽△CAB.正确的有( )
;④△AMN∽△CAB.正确的有( )
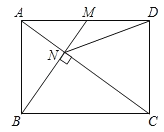
A.①②③④B.①②③C.①②④D.②③④
【答案】C
【解析】
通过证明△AMN∽△CBN,可得![]() ,可证CN=2AN;过D作DH∥BM交AC于G,可证四边形BMDH是平行四边形,可得BH=MD=
,可证CN=2AN;过D作DH∥BM交AC于G,可证四边形BMDH是平行四边形,可得BH=MD=![]() BC,由直角三角形的性质和等腰三角形的性质可得DN=DC;通过证明△ABM∽△BCA,可得
BC,由直角三角形的性质和等腰三角形的性质可得DN=DC;通过证明△ABM∽△BCA,可得![]() ,可求AB=
,可求AB=![]() BC,即可得tan∠DAC=
BC,即可得tan∠DAC=![]() ;由平行线性质可得∠DAC=∠ACB,∠ABC=∠ANM=90°,可证△AMN∽△CAB,则可求解.
;由平行线性质可得∠DAC=∠ACB,∠ABC=∠ANM=90°,可证△AMN∽△CAB,则可求解.
∵AD//BC,
∴△AMN∽△CBN,
∴![]() ,
,
∵M是AD边的中点,
∴AM=MD=![]() AD=
AD=![]() BC,
BC,
∴![]() ,
,
∴CN=2AN,故①正确;
如图,过D作DH//BM交AC于G,
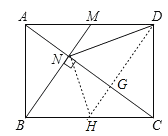
∵DH//BM,BM⊥AC,
∴DH⊥AC,
∵DH//BM,AD//BC,
∴四边形BMDH是平行四边形,
∴BH=MD=![]() AD=
AD=![]() BC,
BC,
∴BH=CH,
∵∠BNC=90°,
∴NH=HC,
∵DH⊥AC,
∴DH是NC的垂直平分线,
∴DN=CD,故②正确;
∵AD//BC,
∴∠DAC=∠BCA,
∵∠BAC+∠ACB=90°,∠DAC+∠AMB=90°,
∴∠BAC=∠AMB,
∵∠BAM=∠ABC,
∴△ABM∽△BCA,
∴![]() ,
,
∴AB2=![]() BC2,
BC2,
∴AB=![]() BC,
BC,
∵tan∠DAC=tan∠ACB=![]() ,
,
∴tan∠DAC=![]() ,故③错误,
,故③错误,
∵四边形ABCD是矩形,
∴AD//BC,∠ABC=90°,AD=BC,
∴∠DAC=∠ACB,
∵∠ABC=∠ANM=90°,
∴△AMN∽△CAB,故④正确;
故选:C.


科目:初中数学 来源: 题型:
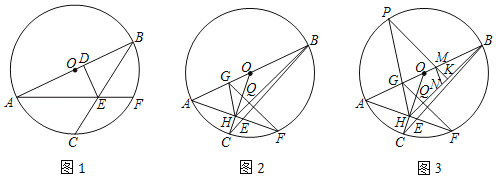
【题目】已知,AB为⊙O的直径,弦BC、AF相交于点E,过点E作ED⊥AB,∠AEC=∠BED.
(1)如图1,求证:![]() ;
;
(2)如图2,当∠BAF=45°时,OC交AF于点H,作FG⊥BH于点Q,交AB于点G,连接GH,求证:∠AGH=∠BGF;
(3)如图3,在(2)的条件下,射线HG与⊙O交于点P,过点P作PK⊥BH交AB于点M,垂足为点K,点N为BH的中点,MN=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
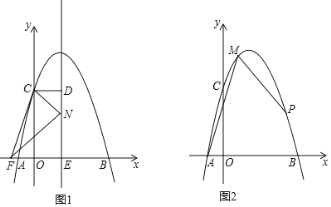
【题目】二次函数y=ax2+bx+4的图象与x轴交于两点A、B,与y轴交于点C,且A(1,0)、B(4,0).
(1)求此二次函数的表达式;
(2)如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(![]() ,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标;
,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标;
(3)如图2,点M在抛物线上,且点M的横坐标是1,点P为抛物线上一动点,若∠PMA=45°,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
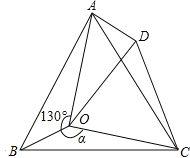
【题目】如图,点O是等边三角形ABC内的一点,∠AOB=130°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.
(1)判断△COD的形状,并加以说明理由.
(2)若AD=1,OC=![]() ,OA=
,OA=![]() 时,求α的度数.
时,求α的度数.
(3)探究:当α为多少度时,△AOD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
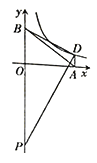
【题目】如图,在平面直角坐标系中,点A、B分别在x轴、y轴的正半轴上,OA=4,AB=5,点D在反比例函数![]() (k>0)的图象上,
(k>0)的图象上,![]() ,点P在y轴负半轴上,OP=7.
,点P在y轴负半轴上,OP=7.
(1)求点B的坐标和线段PB的长;
(2)当![]() 时,求反比例函数的解析式。
时,求反比例函数的解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步
是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步![]() 小路的宽度不计
小路的宽度不计![]() 观测得点B在点A的南偏东
观测得点B在点A的南偏东![]() 方向上,点C在点A的南偏东
方向上,点C在点A的南偏东![]() 的方向上,点B在点C的北偏西
的方向上,点B在点C的北偏西![]() 方向上,AC间距离为400米
方向上,AC间距离为400米![]() 问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?
问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?
![]() 参考数据:
参考数据:![]() ,
,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
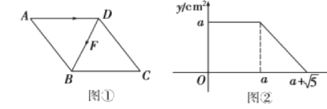
【题目】如图①,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B.图②是点F运动时,△FBC的面积y(cm![]() )随时间x(s)变化的关系图象,则a的值是__
)随时间x(s)变化的关系图象,则a的值是__
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在任意四边形ABCD中,AC,BD是对角线,E、F、G、H分别是线段BD、BC、AC、AD上的点,对于四边形EFGH的形状,某班的学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )

A. 当E,F,G,H是各条线段的中点时,四边形EFGH为平行四边形
B. 当E,F,G,H是各条线段的中点,且AC⊥BD时,四边形EFGH为矩形
C. 当E,F,G,H是各条线段的中点,且AB=CD时,四边形EFGH为菱形
D. 当E,F,G,H不是各条线段的中点时,四边形EFGH可以为平行四边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com