
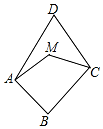
 如图,M是线段AD、CD的垂直平分线交点,AB⊥BC,∠D=55°,则∠MAB+∠MCB的大小是( )
如图,M是线段AD、CD的垂直平分线交点,AB⊥BC,∠D=55°,则∠MAB+∠MCB的大小是( )| A. | 120° | B. | 130° | C. | 140° | D. | 160° |
分析 过M作射线DN,根据角平分线的定义、垂直的定义计算即可.
解答 解:过M作射线DN,
∵M是线段AD、CD的垂直平分线交点,
∴AM=DM,CM=DM,
∴∠DAM=∠ADM,∠DCM=∠CDM,
∴∠MAD+∠MCD=∠ADM+∠CDM=∠ADC,
∵∠ADC=55°,
∴∠MAD+∠MCD=∠ADC=55°,
∴∠AMC=∠AMN+∠CMN=∠DAM+∠ADM+∠DCM+∠CDM=55°+∠ADC=55°+55°=110°
∵AB⊥BC,
∴∠B=90°,
∴∠MAB+∠MCB=360°-∠B-∠AMC=360°-90°-110°=160°,
故选:D.
点评 本题考查的是角平分线的定义,掌握角平分线的定义是解题的关键.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:解答题
| 销售单价(元) | x |
| 销售量y(件) | 1000-10x |
| 销售玩具获得利润w(元) | -10x2+1300x-30000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在数轴上表示下列各数,并按从小到大的顺序用“<”把这些数连接起来.
在数轴上表示下列各数,并按从小到大的顺序用“<”把这些数连接起来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
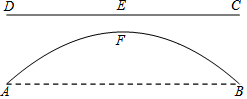 如图,某水库上游有一单孔抛物线型拱桥,它的跨度AB为100米.最低水位(与AB在同一平面)时桥面CD距离水面25米,桥拱两端有两根25米高的水泥柱BC和AD,中间等距离竖立9根钢柱支撑桥面,拱顶正上方的钢柱EF长5米.
如图,某水库上游有一单孔抛物线型拱桥,它的跨度AB为100米.最低水位(与AB在同一平面)时桥面CD距离水面25米,桥拱两端有两根25米高的水泥柱BC和AD,中间等距离竖立9根钢柱支撑桥面,拱顶正上方的钢柱EF长5米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM等于( )
如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM等于( )| A. | 0.5 | B. | 1 | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com