
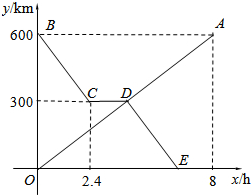
 货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.
货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.分析 (1)待定系数求出OA解析式,继而根据点D的纵坐标为300求得其横坐标,即可得答案;
(2)根据休息前2.4小时行驶300km可得行驶后行驶300km也需要2.4h,即可得点E坐标,待定系数法即可求得DE所在直线解析式;
(3)先求出BC所在直线解析式,再根据①轿车休息前与货车相距200km,②轿车休息后与货车相距200km,分别列出方程求解可得.
解答 解:(1)设OA所在直线解析式为y=mx,
将x=8、y=600代入,求得m=75,
∴OA所在直线解析式为y=75x,
令y=300得:75x=300,解得:x=4,
∴点D 坐标为( 4,300 ),其实际意义为:点D是指货车出发4h后,与轿车在距离甲地300 km处相遇.
(2)由图象知,轿车在休息前2.4小时行驶300km,
∴根据题意,行驶后300km需2.4h,
故点E 坐标( 6.4,0 ).
设DE所在直线的函数表达式为y=kx+b,
将点D ( 4,300 ),E ( 6.4,0)代入y=kx+b得:
$\left\{\begin{array}{l}4k+b=300\\ 6.4k+b=0\end{array}$,
解得 $\left\{\begin{array}{l}b=800\\ k=-125\end{array}$,
∴DE所在直线的函数表达式为y=-125x+800.
(3)设BC段函数解析式为:y=px+q,
将点B(0,600)、C(2.4,300)代入,得:
$\left\{\begin{array}{l}{q=600}\\{2.4p+q=300}\end{array}\right.$,
解得:y=-125x+600,
①当轿车休息前与货车相距200km时,有:-125x+600-75x=200,解得:x=2;
②当轿车休息后与货车相距200km时,有:75x-(-125x+800)=200,解得:x=5;
故答案为:2或5.
点评 本题考查了一次函数的应用,待定系数法是求函数解析式的关键,注意分类讨论思想的渗透.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
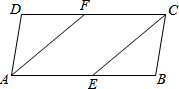 如图,在平行四边形ABCD中,已知AF平分∠DAB,CE平分∠BCD,
如图,在平行四边形ABCD中,已知AF平分∠DAB,CE平分∠BCD,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
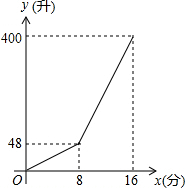 一个容积为400升的水箱,安装有A、B两个注水管,注水过程中A水管始终打开,B水管8分钟后打开,两水管的注水速度均为定值.当水箱注满时,两水管自动停止注水,注水过程中水箱中水量y(升)与A水管注水时间时间x(分)之间的函数图象如图所示.
一个容积为400升的水箱,安装有A、B两个注水管,注水过程中A水管始终打开,B水管8分钟后打开,两水管的注水速度均为定值.当水箱注满时,两水管自动停止注水,注水过程中水箱中水量y(升)与A水管注水时间时间x(分)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥3 | B. | 0≤x≤3 | C. | x≥0 | D. | x>3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
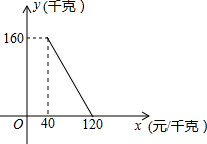 某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售x(元/千克)之间函数关系如图所示.
某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售x(元/千克)之间函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
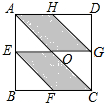 如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )
如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com