

|
|
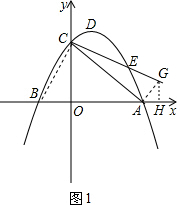
| OB |
| AG |
| OC |
| AC |
| 1 |
| AG |
| 3 | ||
3
|
| 2 |
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 7 |
| 4 |
| 5 |
| 2 |
| 7 |
| 4 |


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 3 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 什么位置时,△PCD的面积是△BCD面积的三分之一,求此时点P的坐标.
什么位置时,△PCD的面积是△BCD面积的三分之一,求此时点P的坐标.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 鲜鱼销售单价(元/kg) | 20 | ||
| 单位捕捞成本(元/kg) | 5-
| ||
| 捕捞量(kg) | 950-10x |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
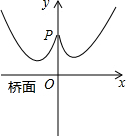 标系,左边的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称.
标系,左边的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com