
已知直线y=kx-3与x轴交于点A(4,0),与y轴交于点C,抛物线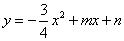 经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.
经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.
(1)求此抛物线的解析式和直线的解析式;
(2)如果点P和点Q同时出发,运动时间为t(秒),试问当t为何值时,以A、P、Q为顶点的三角形与△AOC相似;
 (3)在直线CA上方的抛物线上是否存在一点D,使得△ACD的面积最大.若存在,求出点D的坐标;若不存在,请说明理由.
(3)在直线CA上方的抛物线上是否存在一点D,使得△ACD的面积最大.若存在,求出点D的坐标;若不存在,请说明理由.
解:(1)∵ 直线y=kx-3过点A(4,0),∴ 0 = 4k -3,解得k=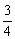 .[来源:学&科&网Z&X&X&K]
.[来源:学&科&网Z&X&X&K]
∴ 直线的解析式为 y=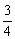 x-3.
x-3.
由直线y=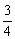 x-3与y轴交于点C,可知C(0,-3) .
x-3与y轴交于点C,可知C(0,-3) .
∴ 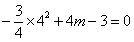 ,解得 m=
,解得 m=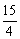 .
.
∴ 抛物线解析式为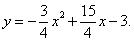
 (2)对于抛物线
(2)对于抛物线 ,
,
令y=0,则 ,解得x1=1,x2=4.
,解得x1=1,x2=4.
∴ B(1,0).
∴ AB=3,AO=4,OC=3,AC=5,AP=3-t,AQ=5-2t.
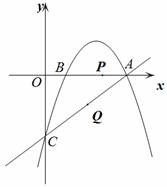
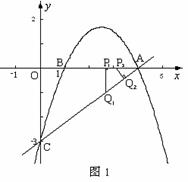
① 若∠Q1P1A=90°,则P1Q1∥OC(如图1),
∴ △AP1Q1∽△AOC.
∴  , ∴
, ∴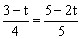 .解得t=
.解得t= 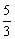 ;
;
② 若∠P2Q2A=90°, ∵∠P2AQ2 =∠OAC,∴ △AP2Q2∽△AOC.
∴ 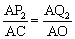 , ∴
, ∴ 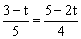 .解得t=
.解得t=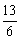 ;
;
综上所述,当t的值为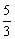 或
或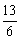 时,以P、Q、A为顶点的三角形与△AOC相似.
时,以P、Q、A为顶点的三角形与△AOC相似.
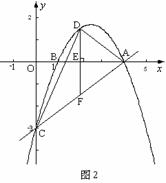 (3)答:存在.
(3)答:存在.
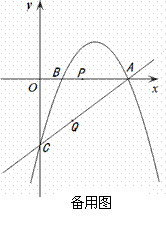
过点D作DF⊥x轴,垂足为E,交AC于点F(如图2).
∴ S△ADF=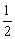 DF·AE,S△CDF=
DF·AE,S△CDF=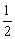 DF·OE.
DF·OE.
∴ S△ACD= S△ADF + S△CDF=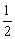 DF×(AE+OE) =
DF×(AE+OE) =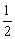 ×4 (DE+EF)
×4 (DE+EF)
=2×( )=
)=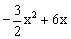 .
.
∴ S△ACD=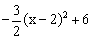 (0<x<4).
(0<x<4).
又0<2<4且二次项系数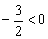 ,∴ 当x=2时,S△
,∴ 当x=2时,S△ ACD的面积最大.
ACD的面积最大.
而当x=2时,y=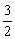 .∴ 满足条件的D点坐标为D (2,
.∴ 满足条件的D点坐标为D (2, 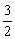 ).
).


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:
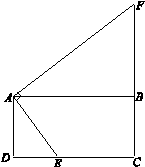
如图,在矩形ABCD中,E是CD边上任意一点(不与点C,D重合),作AF⊥AE交CB的延长线于点F.
(1)求证:△ADE∽△ABF;
(2)连接EF,M为EF的中点,AB=4,AD=2,设DE=x,
①求点M到FC的距离(用含x的代数式表示);
②连接BM,设 ,求y与x之间的函数关系式,并直接写出BM的长度的最小值.
,求y与x之间的函数关系式,并直接写出BM的长度的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com