（1）如图一，等边三角形MNP的边长为1，线段AB的长为4，点M与A重合，点N在线段AB上．△MNP沿线段AB按A→B的方向滚动，直至△MNP中有一个点与点B重合为止，则点P经过的路程为
；
（2）如图三，正方形MNPQ的边长为1，正方形ABCD的边长为2，点M与点A重合，点N在线段AB上，点P在正方形内部，正方形MNPQ沿正方形ABCD的边按A→B→C→D→A→…的方向滚动，始终保持M，N，P，Q四点在正方形内部或边界上，直至正方形MNPQ回到初始位置为止，则点P经过的最短路程为
．
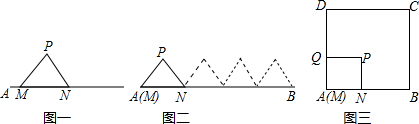
（注：以△MNP为例，△MNP沿线段AB按A→B的方向滚动指的是先以顶点N为中心顺时针旋转，当顶点P落在线段AB上时，再以顶点P为中心顺时针旋转，如此继续．多边形沿直线滚动与此类似．）
解：等边三角形三线合一，
