
分析 (1)设出租车的起步价为x元,超过2千米后每千米收费y元,根据小刘和小李的乘车路程及所付车费,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)根据应付费用=起步价+2×超出2千米的部分(12.3千米按13千米计算),即可求出小张应付车费.
解答 解:(1)设出租车的起步价为x元,超过2千米后每千米收费y元,
根据题意得:$\left\{\begin{array}{l}{x+(5-2)y=14}\\{x+(7-2)y=18}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=8}\\{y=2}\end{array}\right.$.
答:出租车的起步价为8元,超过2千米后每千米收费2元.
(2)8+(13-2)×2=8+22=30(元).
答:小张应付车费30元.
点评 本题考查了二元一次方程组的应用,解题的关键是:(1)找出等量关系,列出二元一次方程组;(2)根据应付费用=起步价+2×超出2千米的部分,列式计算.


科目:初中数学 来源: 题型:解答题
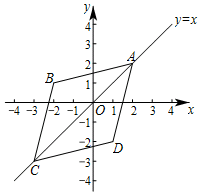 在平面直角坐标系xOy中,如果点A,点C为某个菱形的一组对角的顶点,且点A,C在直线y=x上,那么称该菱形为点A,C的“极好菱形”.如图为点A,C的“极好菱形”的一个示意图.
在平面直角坐标系xOy中,如果点A,点C为某个菱形的一组对角的顶点,且点A,C在直线y=x上,那么称该菱形为点A,C的“极好菱形”.如图为点A,C的“极好菱形”的一个示意图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
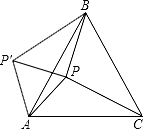 如图,P是等边三角形ABC内的一点,PA=6,PB=8,PC=10.若P′是△ABC外的一点,且△P′AB≌△PAC,求点P与点P′之间的距离及∠APB的度数.
如图,P是等边三角形ABC内的一点,PA=6,PB=8,PC=10.若P′是△ABC外的一点,且△P′AB≌△PAC,求点P与点P′之间的距离及∠APB的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com