

分析 (1)证△APE≌△DPF即可得;
(2)过点N作NQ⊥AD交AD延长线于Q,可得四边形CDQN是矩形,从而表示出PQ、NQ的长,再证△APE∽△QNP可得$\frac{AP}{QN}=\frac{AE}{PQ}$,据此可得函数解析式;
(3)过点N作NQ∥CD交AD延长线于点Q,可得四边形CDQN是平行四边形,据此知PQ=2+x、NQ=4,再过点N作NH⊥PQ于H,由∠DQN=60°得HQ=2、NH=2$\sqrt{3}$,从而表示出PH的长,过点E作EG⊥DA交DA延长线于G,由AE=y、∠GAE=∠B=60°得AG、EG的长,继而可得PG的长,最后证△PEG∽△NPD得$\frac{PG}{NH}=\frac{EG}{PH}$,据此即可得答案.
解答 解:(1)∵P是AD的中点,四边形ABCD是矩形,
∴AP=DP,∠A=∠PDF=90°,
在△APE和△DPF中,
∵$\left\{\begin{array}{l}{∠A=∠PDF}\\{AP=DP}\\{∠APE=∠DPF}\end{array}\right.$,
∴△APE≌△DPF(ASA),
∴PE=PF;
(2)如图1,过点N作NQ⊥AD交AD延长线于Q,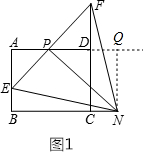
∴四边形CDQN是矩形,
∴CN=DQ=x,CD=NQ=4,
又∵AD=BC=6,P是AD中点,
∴AP=PD=3,
∴PQ=3+x,
∵NP⊥EF,
∴∠APE+∠NPQ=90°,
∵∠APE+∠AEP=90°,
∴∠NPQ=∠PEA,
∵∠A=∠PQN=90°,
∴△APE∽△QNP,
∴$\frac{AP}{QN}=\frac{AE}{PQ}$,即$\frac{3}{4}=\frac{y}{3+x}$,
∴y=$\frac{3}{4}$x+$\frac{9}{4}$;
(3)如图2,过点N作NQ∥CD交AD延长线于点Q,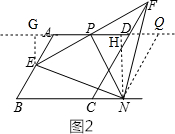
∴四边形CDQN是平行四边形,
∴CN=DQ=x,CD=NQ=4,
∵PD=PA=$\frac{1}{2}$AD=2,
∴PQ=2+x,
过点N作NH⊥PQ于H,
∵∠DQN=∠DCN=∠B=60°,
∴HQ=NQcos∠DQN=4×$\frac{1}{2}$=2,NH=NQsin∠DQN=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴PH=PQ-HQ=x,
过点E作EG⊥DA交DA延长线于G,
∵AE=y,∠GAE=∠B=60°,
∴AG=AEcos∠GAE=$\frac{1}{2}$y,EG=AEsin∠GAE=$\frac{\sqrt{3}}{2}$y,
∴PG=PA+AG=2+$\frac{1}{2}$y,
∵∠EGP=∠PHN=∠EPN=90°,
∴∠EPG+∠PEG=∠EPG+∠NPD=90°,
∴∠PEG=∠NPD,
∴△PEG∽△NPD,
∴$\frac{PG}{NH}=\frac{EG}{PH}$,即$\frac{2+\frac{1}{2}y}{2\sqrt{3}}=\frac{\frac{\sqrt{3}}{2}y}{x}$,
∴y=$\frac{4x}{6-x}$.
点评 本题主要考查全等三角形的判定与性质、矩形与菱形的判定与性质及相似三角形的判定与性质、三角函数的应用,类比思想的运用是解题的关键.


科目:初中数学 来源:2016-2017学年广东省佛山市顺德区七年级3月月考数学试卷(解析版) 题型:单选题
如图,已知∠1=100°,若要使a∥b,则∠2=( )
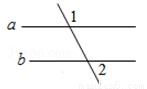
A. 100° B. 60° C. 40° D. 80°
查看答案和解析>>
科目:初中数学 来源:2016-2017学年湖北省枝江市九校七年级3月联考数学试卷(解析版) 题型:单选题
如图,已知AB∥CD,则∠α的度数是( )

A. 60° B. 25° C. 75° D. 85°
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com