
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.

【答案】(1)证明见解析;(2)1.
【解析】分析:(1)只要证明三个角是直角即可解决问题;
(2)作OF⊥BC于F.求出EC、OF的长即可;
详解:(1)证明:∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC=90°,
∴∠BAD=90°,
∴∠BAD=∠ABC=∠ADC=90°,
∴四边形ABCD是矩形.
(2)作OF⊥BC于F.

∵四边形ABCD是矩形,
∴CD=AB=2,∠BCD=90°,AO=CO,BO=DO,AC=BD,
∴AO=BO=CO=DO,
∴BF=FC,
∴OF=![]() CD=1,
CD=1,
∵DE平分∠ADC,∠ADC=90°,
∴∠EDC=45°,
在Rt△EDC中,EC=CD=2,
∴△OEC的面积=![]() ECOF=1.
ECOF=1.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一下正方形.
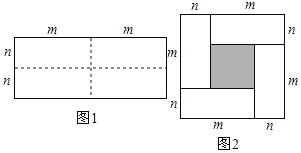
(1)请你用两种不同的方法求图2中阴影部分的面积?
① ②
(2)观察图2,写出三个代数式(m+n)2,(m﹣n)2,4mn之间的等量关系:
(3)根据(2)中的等量关系,解决如下问题:若|a+b﹣7|+|ab﹣6|=0,求(a﹣b)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
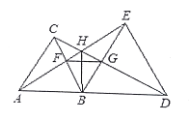
【题目】如图,△ABC和△BDE都是等边三角形,A、B、D三点共线.下列结论:①AE=CD;②BF=BG;③△BFG是等边三角形;④∠AHC=60°.其中正确的有__________(只填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,定义直线
中,定义直线 ![]() 与双曲线
与双曲线 ![]() 的交点
的交点 ![]() (m、n为正整数)为 “双曲格点”,双曲线
(m、n为正整数)为 “双曲格点”,双曲线 ![]() 在第一象限内的部分沿着竖直方向平移或以平行于
在第一象限内的部分沿着竖直方向平移或以平行于 ![]() 轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.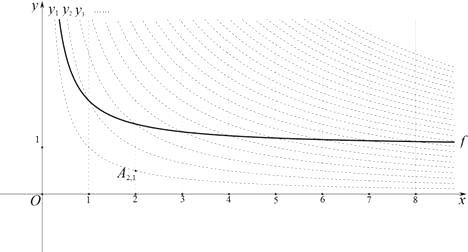
(1)①“双曲格点” ![]() 的坐标为;
的坐标为;
②若线段 ![]() 的长为1个单位长度,则n=;
的长为1个单位长度,则n=;
(2)图中的曲线 ![]() 是双曲线
是双曲线 ![]() 的一条“派生曲线”,且经过点
的一条“派生曲线”,且经过点 ![]() ,则
,则 ![]() 的解析式为 y=;
的解析式为 y=;
(3)画出双曲线 ![]() 的“派生曲线”g(g与双曲线
的“派生曲线”g(g与双曲线 ![]() 不重合),使其经过“双曲格点”
不重合),使其经过“双曲格点” ![]() 、
、 ![]() 、
、 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】货车在公路A处加满油后,以每小时60千米的速度匀速行驶,前往与A处相距360千米的B处.下表记录的是货车一次加满油后油箱剩余油量y(升)与行驶时间x(时)之间的关系:

(1)如果y关于x的函数是一次函数,求这个函数解析式(不要求写出自变量的取值范围)
(2)在(1)的条件下,如果货车的行驶速度和每小时的耗油量都不变,货车行驶4小时后到达C处,C的前方12千米的D处有一加油站,那么在D处至少加多少升油,才能使货车到达B处卸货后能顺利返回会D处加油?(根据驾驶经验,为保险起见,油箱内剩余油量应随时不少于10升)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:
(1)(-78) +(+5)+(+78) (2)(+23)+(-17)+(+6)+(-22)
(3)[45-(![]() -
-![]() +
+![]() )×36]÷5 (4)99
)×36]÷5 (4)99![]() ×(-36)
×(-36)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=kx+b(k≠0)的图象与反比例函数y2=﹣ ![]() 的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.
的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.
(1)求一次函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出y1>y2时x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com