
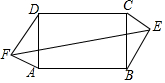
 如图,在矩形ABCD中,AD=5,AB=15,E、F分别为矩形外两点,DF=BE=4,AF=CE=3,则EF等于$\sqrt{394}$.
如图,在矩形ABCD中,AD=5,AB=15,E、F分别为矩形外两点,DF=BE=4,AF=CE=3,则EF等于$\sqrt{394}$. 分析 延长FD交EC的延长线于点M,可证明△MEF是直角三角形,证明△ADF∽△DCM,得出对应边成比例求出CM=3DF=12,DM=3AF=9,得出MF=DF+DM=13,ME=CE+CM=15,在Rt△MEF中,由勾股定理即可求出EF的长.
解答 解:延长FD交EC的延长线于点M,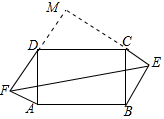 如图所示:
如图所示:
∵四边形ABCD是矩形,
∴CD=AB=15,BC=AD=5,∠BCD=∠ADC=90°,
∵AF=3,DF=4,
∴AF2+DF2=AD2=25
∴△ADF是直角三角形,∠AFD=90°,
同理可证△CBE是直角三角形,
∴∠ADF=∠CBE,∠DAF=∠BCE,∠ADF+∠DAF=90°,∠CBE+∠BCE=90°,
∴∠ADF+∠BCE=90°
又∵∠ADF+∠CDM=90°,∠MCD+∠BCE=90°,
∴∠DMC+∠MCD=90°,∠ADF=∠MCD,
∴∠M=90°=∠AFD,
∴△ADF∽△DCM,
∴$\frac{DF}{CM}=\frac{AF}{CM}=\frac{AD}{CD}$=$\frac{5}{15}$=$\frac{1}{3}$,
∴CM=3DF=12,DM=3AF=9,
∴MF=DF+DM=13,ME=CE+CM=15,
在Rt△MEF中,EF=$\sqrt{M{F}^{2}+M{E}^{2}}$=$\sqrt{1{3}^{2}+1{5}^{2}}$=$\sqrt{394}$;
故答案为:$\sqrt{394}$.
点评 本题考查了正方形的性质、全等三角形的判定和性质以及勾股定理的运用,题目的综合性较强,难度中等,是一道非常不错的中考题目,证明出三角形△EMF是等腰直角三角形是解题的关键.


科目:初中数学 来源: 题型:选择题
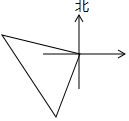 某校八年级生物兴趣小组租两艘快艇去微山湖生物考察,他们从同一码头出发,第一艘快艇沿北偏西70°方向航行50千米,第二艘快艇沿南偏西20°方向航行50千米,如果此时第一艘快艇不动,第二艘快艇向第一艘快艇靠拢,那么第二艘快艇航行的方向和距离分别是( )
某校八年级生物兴趣小组租两艘快艇去微山湖生物考察,他们从同一码头出发,第一艘快艇沿北偏西70°方向航行50千米,第二艘快艇沿南偏西20°方向航行50千米,如果此时第一艘快艇不动,第二艘快艇向第一艘快艇靠拢,那么第二艘快艇航行的方向和距离分别是( )| A. | 南偏东25°,50$\sqrt{2}$千米 | B. | 北偏西25°,50$\sqrt{2}$千米 | ||
| C. | 南偏东70°,100千米 | D. | 北偏西20°,100千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
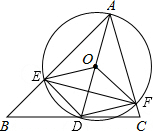 如图,在△ABC中,AB=10$\sqrt{2}$,∠BAC=60°,∠B=45°,点D是BC边上一动点,连接AD,以AD为直径作⊙O交边AB、AC于点E、F,连接OE、OF、DE、DF、EF.
如图,在△ABC中,AB=10$\sqrt{2}$,∠BAC=60°,∠B=45°,点D是BC边上一动点,连接AD,以AD为直径作⊙O交边AB、AC于点E、F,连接OE、OF、DE、DF、EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,网格中的每个小正方形的边长均为1,点A、B在小正方形的顶点上.
如图,网格中的每个小正方形的边长均为1,点A、B在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{50000}{x+400}$=$\frac{50000×(1-20%)}{x}$ | B. | $\frac{50000}{x}$=$\frac{50000×(1-20%)}{x+400}$ | ||
| C. | $\frac{50000}{x-400}$=$\frac{50000×(1-20%)}{x}$ | D. | $\frac{50000}{x}=\frac{50000×(1-20%)}{x-400}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com