
抛物线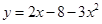 与
与 轴有 个交点,因为其判别式
轴有 个交点,因为其判别式 0,相应二次方程
0,相应二次方程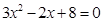 的根的情况为 .
的根的情况为 .
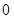 ,
,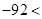 ,没有实数根.
,没有实数根.
【解析】
试题分析:由于抛物线的判别式△=b2-4ac=4-4×(-3)×(-8)=-92<0,由此得到此二次函数与x轴没有交点,也可以得到方程3x2-2x+8=0的根的情况.
∵其判别式b2-4ac=-92<0,
∴抛物线y=2x-8-3x2与x轴有0个交点,
∴相应二次方程3x2-2x+8=0的根的情况为没有实数根.
考点:此题考查了二次函数y=ax2+bx+c的图象和其判别式的关系
点评:解答本题的关键是掌握二次函数y=ax2+bx+c的图象和其判别式的关系:
①当b2-4ac>0时,二次函数与x轴有两个交点;
②当b2-4ac=0时,二次函数与x轴有一个交点;
③当b2-4ac<0时,二次函数与x轴没有交点.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:
已知:抛物线![]() (
(![]() 为常数,且
为常数,且![]() ).
).
(1)求证:抛物线与![]() 轴有两个交点;
轴有两个交点;
(2)设抛物线与![]() 轴的两个交点分别为
轴的两个交点分别为![]() 、
、![]() (
(![]() 在
在![]() 左侧),与
左侧),与![]() 轴的交点为
轴的交点为![]() .
.
①当![]() 时,求抛物线的解析式;
时,求抛物线的解析式;
②将①中的抛物线沿![]() 轴正方向平移
轴正方向平移![]() 个单位(
个单位(![]() >0),同时将直线
>0),同时将直线![]() :
:![]() 沿
沿![]() 轴正方向平移
轴正方向平移![]() 个单位.平移后的直线为
个单位.平移后的直线为![]() ,移动后
,移动后![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() .当
.当![]() 为何值时,在直线
为何值时,在直线![]() 上存在点
上存在点![]() ,使得△
,使得△![]() 为以
为以![]() 为直角边的等腰直角三角形?
为直角边的等腰直角三角形?
查看答案和解析>>
科目:初中数学 来源:2012届河南省南阳市三中九年级下学期第一次月考数学卷 题型:解答题
(8分)已知抛物线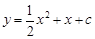 与
与 轴有两个不同的交点.
轴有两个不同的交点.
【小题1】(1)求 的取值范围;
的取值范围;
【小题2】(2)抛物线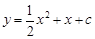 与x轴两交点的距离为2,求
与x轴两交点的距离为2,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(陕西卷)数学(解析版) 题型:解答题
如果一条抛物线 与
与 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.

(1)“抛物线三角形”一定是 三角形;
(2)若抛物线 的“抛物线三角形”是等腰直角三角形,求
的“抛物线三角形”是等腰直角三角形,求 的值;
的值;
(3)如图,△ 是抛物线
是抛物线 的“抛物线三角形”,是否存在以原点
的“抛物线三角形”,是否存在以原点 为对称中心的矩形
为对称中心的矩形 ?若存在,求出过
?若存在,求出过 三点的抛物线的表达式;若不存在,说明理由.
三点的抛物线的表达式;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com