
 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
 如图1,等腰直角△ABC的顶点A,B的坐标分别为(0,10),(8,4),顶点C在第一象限.点P从点A出发,沿△ABC的边按逆时针方向匀速运动,同时,点O从点E(4,0)出发,沿x轴正方向以相同速度运动.当点P到达点C时.P、Q两点同时停止运动,设运动的时间为t秒,
如图1,等腰直角△ABC的顶点A,B的坐标分别为(0,10),(8,4),顶点C在第一象限.点P从点A出发,沿△ABC的边按逆时针方向匀速运动,同时,点O从点E(4,0)出发,沿x轴正方向以相同速度运动.当点P到达点C时.P、Q两点同时停止运动,设运动的时间为t秒,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
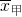 =80,
=80,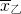 =80,
=80,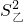 =240,
=240, =180,则测验成绩较整齐的是________班.
=180,则测验成绩较整齐的是________班.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知?ABCD和?AB′C′D有一条公共边AD,它们的对边在同一条直线上.
如图,已知?ABCD和?AB′C′D有一条公共边AD,它们的对边在同一条直线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 树种 | 二氧化碳年平均吸收量(公斤/棵) |
| A种树 | 30 |
| B种树 | 12 |
| C种树 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在⊙O中,CD是直径,AB是弦,AB⊥CD于M,P是弧AD上任一点,CD=20,CM=4.
如图,在⊙O中,CD是直径,AB是弦,AB⊥CD于M,P是弧AD上任一点,CD=20,CM=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com