
如图,AB是⊙O的直径,C为圆周上的一点,过点C的直线MN满足∠MCA=∠CBA.
(1)求证:直线MN是⊙O的切线
(2)过点A作AD⊥MN于点D,交⊙O于点E,已知AB=6,BC=3,求阴影部分的面积.

证明:(1)连接OC,∵AB是⊙O的直径,C 为圆周上的一点,
为圆周上的一点,
∴∠ACB=90°,即∠ACO+∠OCB=90°,
∵OC=OB,∴∠OCB=∠OBC,
又∠MCA=∠ABC,故∠MCA= ∠OCB,
∠OCB,
∴∠ACO+∠MCA=90°,即OC⊥MN,直线MN过点C,
∴直线MN是⊙O的切线.(5分)
(2)连接OE、CE,由(1)OC⊥MN,AD⊥MN,得OC∥AE,
在Rt△ACB中,co sB=
sB=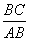 =
=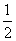 ,∴∠B=60°,故OC=OB=BC=3,
,∴∠B=60°,故OC=OB=BC=3,
∴∠EAO=∠COB=60°,故OE=OA=EA=3,∠EOC=60°,
∴OC=AE,四边形AOCE是平行四边形,故S△EAC=S△EOC(8分)
于是,S阴=S△ADC-S扇形EOC,
在Rt△ACB中,BC=3,AB=6,∴AC=3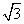 ,
,
在Rt △ADC中,AC=3
△ADC中,AC=3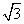 ,∠DCA=∠B=60°,
,∠DCA=∠B=60°,
∴DC=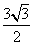 ,AD=
,AD=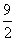 , ∴S△ADC=
, ∴S△ADC=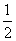 AD·DC=
AD·DC=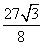 ,(10分)
,(10分)
而S扇形EOC=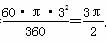 于是S阴=S△ADC-S扇形EOC=
于是S阴=S△ADC-S扇形EOC=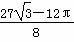


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是( )
A.6 B.10 C.18 D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙、丙、丁4名同学进行一次羽毛球单打比赛,要从中选出2名同学打第一场比赛,求下列事件的概率.
(1) 已确定甲打第一场,再从其余3名同学中随机选取1名,恰好选中乙同学;
(2)随机选取2名同学,其中有乙同学.
查看答案和解析>>
科目:初中数学 来源: 题型:
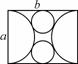
如图,用邻边长分别为a,b(a<b)的矩形硬纸板裁出以a为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆,把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则a与b满足的关系是( )
A. b=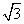 a B.b=
a B.b=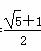 a C.b=
a C.b=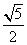 a D. b=
a D. b= a
a
查看答案和解析>>
科目:初中数学 来源: 题型:
将下列正确的命题的序号填在横线上______.
①若n是大于2的正整数,则n边形的所有外角之和为(n- 2)·180°.
2)·180°.
②三角形三条中线的交点就是三角形的重心.
③证明两三角形全等的方法有:SSS,SAS,ASA,SSA及HL等.
查看答案和解析>>
科目:初中数学 来源: 题型:
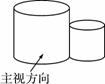
如图所示的物体是由两个紧靠在一起的圆柱组成,小明准备画出它的三视 图,那么他所画的三视图中的俯视图应该是( )
图,那么他所画的三视图中的俯视图应该是( )
A.两个外切的圆 B. 两个内切的圆 C. 两个相交的圆 D. 两个外离的圆
查看答案和解析>>
科目:初中数学 来源: 题型:
为了保护人类居住环境,我国的火电企业积极做好节能环保工作.2011年,我国火电企业的 平均煤耗继续降低,仅为330 000毫克/千瓦时,用科学记数法表示并保留三个有效数字为________毫克/千瓦时.
平均煤耗继续降低,仅为330 000毫克/千瓦时,用科学记数法表示并保留三个有效数字为________毫克/千瓦时.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com