

分析 (1)根据有一个角是直角的平行四边形进行判断;当α=90°时,就是长与宽的比;
(2)在四边形OABC旋转过程中,当0<a≤180°时,是否存在这样的点P和点Q,使BP=$\frac{1}{2}$BQ.构造全等三角形和直角三角形,运用勾股定理求得PC的长,进一步求得坐标.
解答 解:(1)∵点A的坐标为(-8,0),直线BC经过点B(-8,6),C(0,6),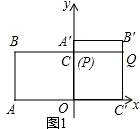
∴BC=AO=8,BC∥AO,
∴四边形OABC是平行四边形.
又OC⊥OA,
∴平行四边形OABC的形状是矩形;
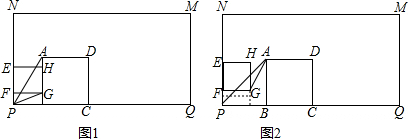
当α=90°时,P与C重合,如图1,
BP=8,BQ=BP+OC=8+6=14,则$\frac{BP}{BQ}$=$\frac{8}{14}$=$\frac{4}{7}$.
故答案是:矩形、$\frac{4}{7}$;
(3)存在这样的点P和点Q,使BP=$\frac{1}{2}$BQ.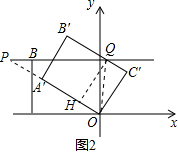
理由如下:过点Q画QH⊥OA′于H,连接OQ,则QH=OC′=OC,
∵S△POQ=$\frac{1}{2}$PQ•OC,S△POQ=$\frac{1}{2}$OP•QH,
∴PQ=OP.
设BP=x,∵BP=$\frac{1}{2}$BQ,
∴BQ=2x,
如图2,当点P在点B左侧时,
OP=PQ=BQ+BP=3x,
在Rt△PCO中,(8+x)2+62=(3x)2,
解得x1=1+$\frac{3\sqrt{6}}{2}$,x2=1-$\frac{3\sqrt{6}}{2}$,(不符实际,舍去).
∴PC=BC+BP=9+$\frac{3\sqrt{6}}{2}$,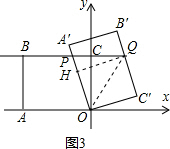
∴P1(-9-$\frac{3\sqrt{6}}{2}$,6),
如图3,当点P在点B右侧时,
∴OP=PQ=BQ-BP=x,PC=8-x.
在Rt△PCO中,(8-x)2+62=x2,解得x=$\frac{25}{4}$,
∴PC=BC-BP=8-$\frac{25}{4}$=$\frac{7}{4}$,
∴P2(-$\frac{7}{4}$,6),
综上可知,存在点P1(-9-$\frac{3\sqrt{6}}{2}$,6),P2(-$\frac{7}{4}$,6)使BP=$\frac{1}{2}$BQ.
故答案为(-9-$\frac{3\sqrt{6}}{2}$,6),P2(-$\frac{7}{4}$,6).
点评 本题考查了旋转的性质,矩形的性质,勾股定理.特别注意在旋转的过程中的对应线段相等,能够用一个未知数表示同一个直角三角形的未知边,根据勾股定理列方程求解.


科目:初中数学 来源: 题型:填空题
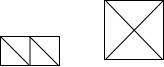 如图,将两个边长为$\sqrt{3}$的正方形对角线剪开,将所得的四个三角形拼成一个大的正方形,则这个大正方形的边长是$\sqrt{6}$.
如图,将两个边长为$\sqrt{3}$的正方形对角线剪开,将所得的四个三角形拼成一个大的正方形,则这个大正方形的边长是$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
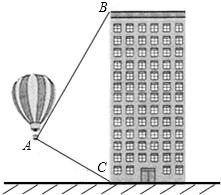 小明和小华准备利用迷你热气球来测量如图所示的高楼BC的高度,从热气球探测到此高楼顶部的仰角为66°,此高楼底部的俯角为36°,此时热气球距离C的距离是42米,请计算这栋高楼的高度是多少米(sin66°≈0.90,cos66°≈0.40,tan66°≈2.25,sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
小明和小华准备利用迷你热气球来测量如图所示的高楼BC的高度,从热气球探测到此高楼顶部的仰角为66°,此高楼底部的俯角为36°,此时热气球距离C的距离是42米,请计算这栋高楼的高度是多少米(sin66°≈0.90,cos66°≈0.40,tan66°≈2.25,sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
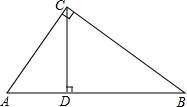 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.则下列等式正确的个数有( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.则下列等式正确的个数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9π | B. | 16π | C. | 27π | D. | 36π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com