
【题目】爸爸为了检查小明对平行线的条件与性质这部分知识的掌握情况,给他出了一道题:如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE的度数.小明稍加思索,就做出来了,你知道他是怎样解的吗?请把你的推理过程写下来吧. 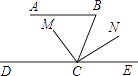
【答案】解:∵AB∥DE,∠B=80° ∴∠B+∠DCB=180°,
∴∠DCB=180°﹣80°=100°,
∵CM平分∠BCD,
∴∠DCM= ![]() ∠BCD=
∠BCD= ![]() ×100°=50°,
×100°=50°,
∵CM⊥CN,
∴∠MCN=90°,
∴∠ECN=180°﹣90°﹣50°=40°.
【解析】先根据AB∥DE,得出∠B+∠DCB=180°,故可得出∠DCB的度数,再根据CM平分∠BCD,可知∠DCM= ![]() ∠BCD,由CM⊥CN,可知∠MCN=90°,根据∠ECN=180°﹣∠MCN﹣∠DCM即可得出结论.
∠BCD,由CM⊥CN,可知∠MCN=90°,根据∠ECN=180°﹣∠MCN﹣∠DCM即可得出结论.
【考点精析】掌握垂线的性质和平行线的性质是解答本题的根本,需要知道垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,CF是∠ACB的平分线,CG是∠ACB外角的平分线,FG∥BC交CG于点G,已知∠A=45°,∠B=55°,求∠FGC和∠FCG的度数. 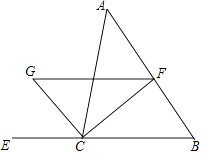
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC中,AB=AC,∠B=α.
(1)如图1,点D,E分别在边AB,AC上,线段DE的垂直平分线MN交直线BC于点M,交DE于点N,求证:BD+CE=BC.需补充条件∠EMN=(用含α的式子表示)补充条件后并证明;
(2)把(1)中的条件改为点D,E分别在边BA、AC延长线上,线段DE的垂直平分线MN交直线BC于点M,交DE于点N(如图2),并补充条件∠EMN=(用含α的式子表示),通过观察或测量,猜想线段BD,CE与BC之间满足的数量关系,并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在∠AOB内有一点P.
(1)过P画l1∥OA;过P画l2∥OB;
(2)猜想l1与l2相交的角与∠O的大小有怎样关系?(可以用量角器量一下)
(3)你能用你所学的知识证明(3)的结论吗? 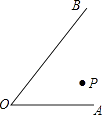
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是( ) 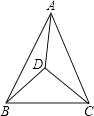
A.100°
B.80°
C.70°
D.50°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com