
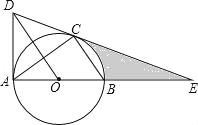
【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AE=6,CE=2![]() ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
【答案】(1)证明见解析;
(2)S阴影部分=2![]() ﹣
﹣![]() π.
π.
【解析】
试题分析:(1)连结OC,如图,先根据切线的性质得∠BAD=90°,再根据平行线的性质,由OD∥BC得∠1=∠3,∠2=∠4,加上∠3=∠4,则∠1=∠2,接着证明△AOD≌△COD,得到∠OCD=∠OAD=90°,于是可根据切线的判定定理得到DE是⊙O的切线;
(2)设半径为r,则OE=AE﹣OA=6﹣r,OC=r,在Rt△OCE中利用勾股定理得到r2+(2![]() )2=(6﹣r)2,解得r=2,再利用正切函数求出∠COE=60°,然后根据扇形面积公式和S阴影部分=S△COE﹣S扇形BOC进行计算即可.
)2=(6﹣r)2,解得r=2,再利用正切函数求出∠COE=60°,然后根据扇形面积公式和S阴影部分=S△COE﹣S扇形BOC进行计算即可.
试题解析:(1)连结OC,如图,∵AD为⊙O的切线,∴AD⊥AB,∴∠BAD=90°,
∵OD∥BC,∴∠1=∠3,∠2=∠4,∵OB=OC,∴∠3=∠4,∴∠1=∠2,
在△OCD和△OAD中,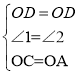 ,∴△AOD≌△COD(SAS);
,∴△AOD≌△COD(SAS);
∴∠OCD=∠OAD=90°,∴OC⊥DE,∴DE是⊙O的切线;
(2)设半径为r,则OE=AE﹣OA=6﹣r,OC=r,在Rt△OCE中,∵OC2+CE2=OE2,
∴r2+(2![]() )2=(6﹣r)2,解得r=2,∵tan∠COE=
)2=(6﹣r)2,解得r=2,∵tan∠COE=![]() =
=![]() =
=![]() ,
,
∴∠COE=60°,∴S阴影部分=S△COE﹣S扇形BOC=![]() ×2×2
×2×2![]() ﹣
﹣![]()
=2![]() ﹣
﹣![]() π.
π.


科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用普查方式的是( )
A. 调查某班级的每一个同学所穿鞋子的尺码情况
B. 调查某批次烟花爆竹的燃放效果
C. 调查奶茶市场上奶茶的质量情况
D. 调查重庆中学生心里健康现状
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】空气是由多种气体混合而成的,为了直观地介绍空气各成分的百分比,最适合使用的统计图是______(从“条形图,扇形图,折线图和直方图”中选一个)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市平均每天产生垃圾700 t,由甲、乙两家垃圾处理厂处理.已知甲厂每小时可处理垃圾55 t,费用为550元;乙厂每小时可处理垃圾45 t,费用为495元.
(1)如果甲、乙两厂同时处理该城市的垃圾,那么每天需几小时?
(2)如果该城市规定每天用于处理垃圾的费用不得高于7370元,那么至少安排甲厂处理几小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
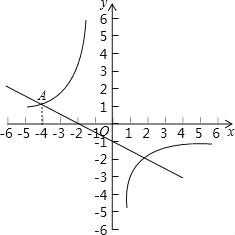
【题目】如图,观察图象,回答问题:
(1)点D的纵坐标等于____.
(2)点A的横坐标是方程______的解.
(3)大于点B横坐标的x的值是不等式________的解.
(4)点C的横、纵坐标是方程组_________的解.
(5)小于点C横坐标的x的值是不等式__________的解.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=x2+3先向左平移2个单位,再向下平移1个单位,所得新抛物线的解析式为( )
A.y=(x+2)2+2B.y=(x﹣1)2+5C.y=(x+2)2+4D.y=(x﹣2)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论不正确的是( )
A.若a<0,b>0,则a-b<0
B.若a>0,b<0,则a-b>0
C.若a<0,b<0,则a-(-b)>0
D.若a<0,b<0,且|a|>|b|,则a-b<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y1=﹣![]() x﹣1与反比例函数y2=
x﹣1与反比例函数y2=![]() 的图象交于点A(﹣4,m).
的图象交于点A(﹣4,m).
(1)观察图象,在y轴的左侧,当y1>y2时,请直接写出x的取值范围;
(2)求出反比例函数的解析式.
(3)求直线与双曲线的另一个交点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com