
 已知将一矩形纸片ABCD折叠,使顶点A与C重合,折痕为EF.
已知将一矩形纸片ABCD折叠,使顶点A与C重合,折痕为EF.分析 (1)由将一矩形纸片ABCD折叠,使顶点A与C重合,易得∠1=∠2=∠3,即可证得结论;
(2)首先连接AF,由矩形纸片ABCD折叠,易证四边形AFCE为平行四边形;在Rt△CED中,设DE为x,则CE为16-x,CD=AB=8cm,根据勾股定理列方程可求得DE,CE的长;然后由CF=CE,可得CF的长;再运用平行四边形面积公式计算CF×CD可得四边形AFCE的面积.
解答  (1)证明:∵矩形纸片ABCD折叠,顶点A与C重合,折痕为EF,
(1)证明:∵矩形纸片ABCD折叠,顶点A与C重合,折痕为EF,
∴∠1=∠2,AD∥BC,
∴∠1=∠3,
∴∠2=∠3,
∴CE=CF;
(2)解:连接AF,
∵AD∥BC,AE=CE=CF,
∴四边形AFCE为平行四边形,
设DE为xcm,则CE为(16-x)cm,CD=AB=8cm,
在Rt△CDE中,CD2+DE2=CE2,
∴x2+82=(16-x)2,
解得:x=6,
∴DE=6cm,CE=10cm,
∴CF=CE=10cm,
∴S四边形AFCE=CF•CD=10×8=80(cm2).
点评 此题考查了折叠的性质、矩形的性质以及勾股定理的应用.注意利用方程思想求解是关键.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:解答题
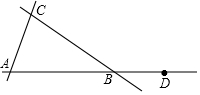 如图,三个村庄A,B,C分别位于三条公路的两两交汇处,形成△ABC,且BA=BC,现计划修建一个粮仓G满足以下两个条件:①在∠CBD的平分线上;②在边BC的中线AF所在的直线上,请用尺规画出粮仓G的位置(不写画法,但要保留作图痕迹,在图中标明相应的字母);BG与边AC的位置关系怎样?
如图,三个村庄A,B,C分别位于三条公路的两两交汇处,形成△ABC,且BA=BC,现计划修建一个粮仓G满足以下两个条件:①在∠CBD的平分线上;②在边BC的中线AF所在的直线上,请用尺规画出粮仓G的位置(不写画法,但要保留作图痕迹,在图中标明相应的字母);BG与边AC的位置关系怎样?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 阅读纸质书籍的数量(本) | 3 | 7 | 11 | 15 |
| 人数 | 4 | 8 | 10 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com