
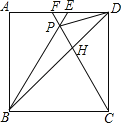
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③DP2=PHPC;④FE:BC=![]() ,其中正确的个数为( )
,其中正确的个数为( )
A.1B.2C.3D.4
【答案】D
【解析】
由正方形的性质和相似三角形的判定与性质,即可得出结论.
解:∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
∴BE=2AE;故①正确;
∵PC=CD,∠PCD=30°,
∴∠PDC=75°,
∴∠FDP=15°,
∵∠DBA=45°,
∴∠PBD=15°,
∴∠FDP=∠PBD,
∵∠DFP=∠BPC=60°,
∴△DFP∽△BPH;故②正确;
∵∠PDH=∠PCD=30°,∠DPH=∠DPC,
∴△DPH∽△CPD,
∴![]() ,
,
∴DP2=PHPC,故③正确;
∵∠ABE=30°,∠A=90°
∴AE=![]() AB=
AB=![]() BC,
BC,
∵∠DCF=30°,
∴DF=![]() DC=
DC=![]() BC,
BC,
∴EF=AE+DF=![]() ﹣BC,
﹣BC,
∴FE:BC=(2![]() ﹣3):3
﹣3):3
故④正确,
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() (x>0)交于点
(x>0)交于点![]() .
.
(1)求a,k的值;
(2)已知直线![]() 过点
过点![]() 且平行于直线
且平行于直线![]() ,点P(m,n)(m>3)是直线
,点P(m,n)(m>3)是直线![]() 上一动点,过点P分别作
上一动点,过点P分别作![]() 轴、
轴、![]() 轴的平行线,交双曲线
轴的平行线,交双曲线![]() (x>0)于点
(x>0)于点![]() 、
、![]() ,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为
,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为![]() .横、纵坐标都是整数的点叫做整点.
.横、纵坐标都是整数的点叫做整点.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点个数;②若区域
内的整点个数;②若区域![]() 内的整点个数不超过8个,结合图象,求m的取值范围.
内的整点个数不超过8个,结合图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
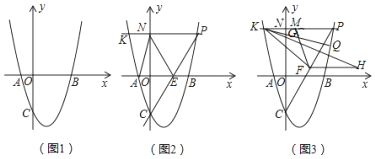
【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c交x轴于A(﹣1,0),B(3,0)两点,交y轴于点C.
(1)如图1,求抛物线的解析式;
(2)如图2,点P是第一象限抛物线上的一个动点,连接CP交x轴于点E,过点P作PK∥x轴交抛物线于点K,交y轴于点N,连接AN、EN、AC,设点P的横坐标为t,四边形ACEN的面积为S,求S与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,点F是PC中点,过点K作PC的垂线与过点F平行于x轴的直线交于点H,KH=CP,点Q为第一象限内直线KP下方抛物线上一点,连接KQ交y轴于点G,点M是KP上一点,连接MF、KF,若∠MFK=∠PKQ,MP=AE+![]() GN,求点Q坐标.
GN,求点Q坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
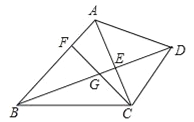
【题目】已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GEGD.
(1)求证:∠ACF=∠ABD;
(2)连接EF,求证:EFCG=EGCB.
查看答案和解析>>
科目:初中数学 来源: 题型:
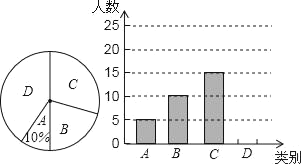
【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤50 | a |
C | 51≤m≤75 | 50 |
D | m≥76 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为 ,a= ;
(2)随机抽取一位学生进行调查,刚好抽到A类学生的概率是 ;
(3)若该校有2000名学生,请估计全校学生中家庭藏书不少于76本的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
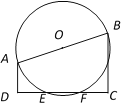
【题目】如图,梯形ABCD中,AD∥BC,∠ADC=90,AD= 2,BC= 4,![]() .以AB为直径作⊙O,交边DC于E、F两点.
.以AB为直径作⊙O,交边DC于E、F两点.
(1)求证:DE=CF.
(2)求直径AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
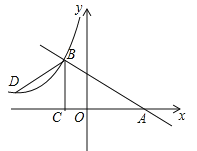
【题目】如图,已知一次函数y=kx+b的图象与x轴交于点A,与反比例函数![]() (x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(1)求m的值;
(2)若∠DBC=∠ABC,求一次函数y=kx+b的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一副三角板中含有30°角的三角板的直角顶点落在等腰直角三角形的斜边的中点D处,并绕点D旋转,两直角三角板的两直角边分别交于点E,F,下列结论:①DE=DF;②S四边形AEDF=S△BED+S△CFD;③S△ABC=EF2;④EF2=BE2+CF2,其中正确的序号是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
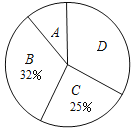
【题目】某市三景区是人们节假日游玩的热点景区,某学校对九(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了不完全的条形统计图和扇形统计图如下:
请结合图中信息解答下列问题:
(1)九(1)班现有学生 人,在扇形统计图中表示“B类别”的扇形的圆心角的度数为 ;
(2)请将条形统计图补充完整;
(3)若该校九年级有1000名学生,求计划“五一”小长假随父母到这三个景区游玩的学生多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com