
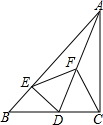
 如图,在Rt△ABC中,∠ACB=90°,D是边BC上一动点(不与B,C重合),DE⊥AB于点E,点F是线段AD的中点,连接EF,CF.
如图,在Rt△ABC中,∠ACB=90°,D是边BC上一动点(不与B,C重合),DE⊥AB于点E,点F是线段AD的中点,连接EF,CF.分析 (1)EF和CF分别是直角△AED和直角△ACD斜边上的中线,依据直角三角形斜边上的中线等于斜边的一半即可证得;
(2)证明△EFC是等边三角形,然后根据等边三角形的定义以及直角三角形的性质求解.
解答  解:(1)EF=CF,
解:(1)EF=CF,
在Rt△AED和Rt△ACD中,
∵点F是线段AD的中点,
∴EF=$\frac{1}{2}$ AD,CF=$\frac{1}{2}$AD,
∴EF=CF.
(2)由(1)可知EF=AF=CF,
∴∠AEF=∠EAF,∠ACF=∠CAF,
∴∠EFD=2∠EAF,∠CFD=2∠CAF,
∴∠EFC=2∠BAC=60°,
又EF=CF,
∴△EFC为等边三角形,
∴CE=EF=$\frac{1}{2}$ AD.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半以及等边三角形的判定与性质,证得△EFC是等边三角形是关键.


科目:初中数学 来源:2017届江苏省无锡市九年级下学期第一次模拟考试数学试卷(解析版) 题型:单选题
下图是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,那么这个几何体的主视图是( )
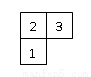
A. 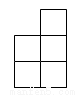 B.
B.  C.
C. 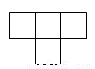 D.
D. 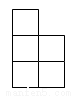
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
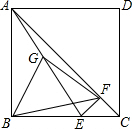 在正方形ABCD中.
在正方形ABCD中.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间/t(min) | 1 | 2.5 | 5 | 10 | 20 | 50 | … |
| 路程/s(km) | 2 | 5 | 10 | 20 | 40 | 100 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com