
 两个完全重合的直角三角形Rt△ABC与Rt△DEF两直角边分别为3cm、4cm,点D放置在AB的中点,△DEF可以绕点D转动,当Rt△DEF旋转到一边与AB垂直时,两三角形重叠部分面积为$\frac{75}{64}$、$\frac{69}{32}$、$\frac{25}{12}$.
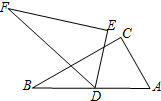
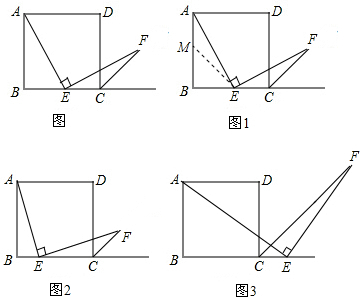
两个完全重合的直角三角形Rt△ABC与Rt△DEF两直角边分别为3cm、4cm,点D放置在AB的中点,△DEF可以绕点D转动,当Rt△DEF旋转到一边与AB垂直时,两三角形重叠部分面积为$\frac{75}{64}$、$\frac{69}{32}$、$\frac{25}{12}$. 分析 分三种情况讨论:①如图1,当DF⊥AB时,重叠部分面积为梯形面积,求出MC、DH和CH代入面积公式计算即可;
②如图2,当DE⊥AB时,重叠部分面积为△DMN的面积,求出MN和DG的长;
③如图3,当EF⊥AB时,重叠部分面积为△ADH的面积,求出AD和GH的长.
解答  解:分三种情况:①如图1,当DF⊥AB时,则DE⊥AC
解:分三种情况:①如图1,当DF⊥AB时,则DE⊥AC
∴DE∥CB
则DE=$\frac{1}{2}$BC=2,CH=$\frac{1}{2}$AC=$\frac{3}{2}$
∵∠B=∠B,∠BDM=∠BCA=90°
∴△BDM∽△BCA
∴$\frac{BM}{AB}$=$\frac{BD}{BC}$
∴$\frac{BM}{5}$=$\frac{2.5}{4}$
∴BM=$\frac{25}{8}$
∴CM=BC-BM=4-$\frac{25}{8}$=$\frac{7}{8}$
∴S重叠部分=S梯形CHDM=$\frac{1}{2}$×($\frac{7}{8}$+2)×$\frac{3}{2}$=$\frac{69}{32}$
②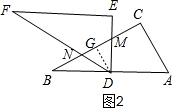 如图2,当DE⊥AB时,则EF∥AB,
如图2,当DE⊥AB时,则EF∥AB,
∴∠F=∠FDB,
过D作DG⊥BC,垂足为G,则AC∥DG,
∵D是BC的中点,
∴G是BC的中点,
∴DG=$\frac{1}{2}$AC=$\frac{3}{2}$,BG=CG=2,
∵∠F=∠B=∠FDB,
∴BN=ND,
设DN=x,则BN=DN=x,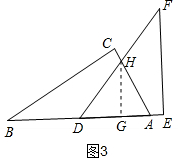
∴(2-x)2+$(\frac{3}{2})^{2}$=x2,
x=$\frac{25}{16}$,
∴BN=$\frac{25}{16}$,
由①得BM=$\frac{25}{8}$,
∴MN=BM-BN=$\frac{25}{8}$-$\frac{25}{16}$=$\frac{25}{16}$,
∴S重叠部分=S△DMN=$\frac{1}{2}$×MN×DG=$\frac{1}{2}$×$\frac{25}{16}$×$\frac{3}{2}$=$\frac{75}{64}$;
③如图3,当EF⊥AB时,
过H作HG⊥AB,则HG∥EF,
∵△ABC≌△DFE,
∴∠FDE=∠CAB,
∴AH=DH,
∴DG=AG=$\frac{1}{4}$AB=$\frac{5}{4}$,
又∵$\frac{DG}{DE}=\frac{GH}{EF}$,
∴$\frac{\frac{5}{4}}{3}$=$\frac{GH}{4}$,GH=$\frac{5}{3}$,
∴S重叠部分=S△ADH=$\frac{1}{2}$×AD×GH=$\frac{1}{2}$×$\frac{5}{2}$×$\frac{5}{3}$=$\frac{25}{12}$;
综上所述:重叠部分的面积为:$\frac{27}{16}$、$\frac{69}{32}$、$\frac{25}{12}$;
故答案为:$\frac{75}{64}$、$\frac{69}{32}$、$\frac{25}{12}$.
点评 本题考查了旋转的性质,正确画出图形是本题的关键;同时运用了分类讨论的思想,确定重叠部分的图形后再利用勾股定理和相似三角形对应边的比求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,C在以AB为直径的半圆⊙O上,I是△ABC的内心,AI,BI 的延长线分别交半圆⊙O于点D,E,AB=6,则DE的长为( )
如图,C在以AB为直径的半圆⊙O上,I是△ABC的内心,AI,BI 的延长线分别交半圆⊙O于点D,E,AB=6,则DE的长为( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3a2b-a2b=2 | |
| B. | 单项式-x2的系数是-1 | |
| C. | 使式子$\frac{{a}^{2}-1}{a+1}$有意义的x的取值范围是x>-1 | |
| D. | 若分式$\frac{{a}^{2}-1}{a+1}$的值等于0,则a=±1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com