
【题目】如图,已致点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() .过点
.过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ;过点
;过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ;过点
;过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ;……;按此规律进行下去,则点
;……;按此规律进行下去,则点![]() 的坐标为( )
的坐标为( )
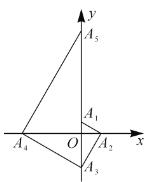
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70--79分为生产技能良好,60--69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | 75 |
乙 | 78 | 80.5 | 81 |
售价 | 50 | 60 | 70 |
销售量 | 120 | 100 | 80 |
(1)求![]() 与
与![]() 之间的函数表达式.
之间的函数表达式.
(2)设该商品每天的总利润为![]() (元),则当售价
(元),则当售价![]() 定为多少元/千克时,超市每天能获得最大利润?最大利润是多少元?
定为多少元/千克时,超市每天能获得最大利润?最大利润是多少元?
(3)如果超市要获得每天不低于1600元的利润,且符合超市自己的规定,那么该商品的售价![]() 的取值范围是多少?请说明理由.
的取值范围是多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年我国个人所得税征收办法最新规定:月收入不超过
年我国个人所得税征收办法最新规定:月收入不超过![]() 元的部分不收税;月收入超过
元的部分不收税;月收入超过![]() 元但不超过
元但不超过![]() 元的部分征收
元的部分征收![]() 的所得税;月收入超过
的所得税;月收入超过![]() 元但不超过
元但不超过![]() 元的部分征收
元的部分征收![]() 的所得税
的所得税![]() 国家特别规定月收入指个人工资收入扣除专项附加费后的实际收入(专项附加费就是子女教育费用、住房贷款利息费用、租房的租金、赡养老人、大病医疗费用等费用).如某人月工资收入
国家特别规定月收入指个人工资收入扣除专项附加费后的实际收入(专项附加费就是子女教育费用、住房贷款利息费用、租房的租金、赡养老人、大病医疗费用等费用).如某人月工资收入![]() 元,专项附加费支出
元,专项附加费支出![]() 元,他应缴纳个人所得税为:
元,他应缴纳个人所得税为:![]() (元).
(元).
(1)当月收入超过![]() 元而又不超过
元而又不超过![]() 元时,写出应缴纳个人所得税
元时,写出应缴纳个人所得税![]() (元)与月收入
(元)与月收入![]() (元)之间的关系式;
(元)之间的关系式;
(2)如果某人当月专项附加费支出![]() 元,缴纳个人所得税
元,缴纳个人所得税![]() 元,那么此人本月工资是多少元?
元,那么此人本月工资是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平而直角坐标系中,一次函数y=﹣4x+4的图象与x轴、y轴分别交于A、B两点.正方形ABCD的项点C、D在第一象限,顶点D在反比例函数y=![]() (k≠0)的图象上.若正方形ABCD向左平移n个单位后,顶点C恰好落在反比例函数的图象上,则n的值是( )
(k≠0)的图象上.若正方形ABCD向左平移n个单位后,顶点C恰好落在反比例函数的图象上,则n的值是( )
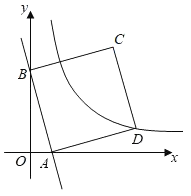
A.2B.3C.4.D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为
S3;则S3﹣S2= .
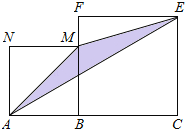
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com