
����Ŀ���¶��壺���ڹ���![]() �ĺ���
�ĺ���![]() ���dzƺ���
���dzƺ���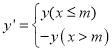 Ϊ����
����![]() ��
��![]() �ֺ���(����
�ֺ���(����![]() Ϊ����)��
����)��
���磺���ڹ���![]() ��һ�κ���
��һ�κ���![]() ��
��![]() �ֺ���Ϊ
�ֺ���Ϊ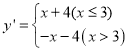
��1������![]() �ڹ���
�ڹ���![]() ��һ�κ���
��һ�κ���![]() ��
��![]() �ֺ����ϣ���
�ֺ����ϣ���![]() ��ֵ��
��ֵ��
��2�������������![]() ��
��![]() �ֺ�����ͼ����
�ֺ�����ͼ����![]() ��
��![]() �����������
���������С��![]() ��ȡֵ��Χ ��
��ȡֵ��Χ ��
��3����![]() �Ƕ��κ���
�Ƕ��κ���![]() ����
����![]() ��
��![]() �ֺ�����
�ֺ�����
![]() ��
��![]() ʱ����
ʱ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
![]() ��
��![]() ʱ��
ʱ��![]() ��
��![]() ��ȡֵ��ΧΪ ��
��ȡֵ��ΧΪ ��
��4������![]() ����
����![]() ������
������![]() �Ķ��κ���
�Ķ��κ���![]() ��
��![]() �ֺ��������߶�
�ֺ��������߶�![]() ���������㣬ֱ��д��
���������㣬ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1��![]() ��2��
��2��![]() ��
��![]() ��3����
��3����![]() ��
��![]() ��
��![]() ��4��m��1��
��4��m��1��![]() ��m��
��m��![]() ��m��4
��m��4
��������
��1����������д��һ�κ���y��x��1��2�ֺ���Ϊy'����x=4���뼴����⣻
��2���������������������![]() ��
��![]() �ֺ���y'�����ݷ�����������ͼ���жϣ�
�ֺ���y'�����ݷ�����������ͼ���жϣ�
��3���ٸ�������д�����κ���![]() ����
����![]() ��
��![]() �ֺ���y'������
�ֺ���y'������![]() �ֶμ�����⣻
�ֶμ�����⣻
�����������![]() ʱ��
ʱ��![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ![]() ����
����![]() ʱ��
ʱ��![]() ��֪�����
��֪�����![]() ʱ
ʱ![]() ��ֵ��-3��-4������-3��-4��֮���Ӧ��x��ȡֵ��Χ���ɣ�
��ֵ��-3��-4������-3��-4��֮���Ӧ��x��ȡֵ��Χ���ɣ�
��4����д�����κ���![]() ����
����![]() ��m�ֺ���y'����x23x3��1ʱ��x��1��x��4����x2��span>3x��3��1ʱ��x��
��m�ֺ���y'����x23x3��1ʱ��x��1��x��4����x2��span>3x��3��1ʱ��x��![]() ��x��
��x��![]() ����y��x23x3���߶�ABû�н��㣬m��1����y��x23x3���߶�AB��һ�����㣬y��x2��3x��3���߶�AB��һ�����㣬
����y��x23x3���߶�ABû�н��㣬m��1����y��x23x3���߶�AB��һ�����㣬y��x2��3x��3���߶�AB��һ�����㣬![]() ��m��
��m��![]() ����y��x23x3���߶�AB���������㣬m��4��
����y��x23x3���߶�AB���������㣬m��4��
��1��һ�κ���y��x��1��2�ֺ���Ϊ![]()
![]()
![]() ��
��![]() ����
����![]() ��
��![]()
![]() ��
��
��2������������![]() ��4�ֺ���Ϊ
��4�ֺ���Ϊ ��
��
��y��x���������Сʱ��![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
��3�����κ���y��x22x3����x��1�ֺ���Ϊ
�ٵ�1��x��2ʱ��
1��x��1��y'=![]() ��y��ȡֵ��ΧΪ4��y'��0��
��y��ȡֵ��ΧΪ4��y'��0��
1��x��2��y'=![]() ��y��ȡֵ��ΧΪ3��y'��4��
��y��ȡֵ��ΧΪ3��y'��4��
�൱1��x��2ʱ��y'��ȡֵ��ΧΪ4��y'��0��3��y'��4��
��img src="http://thumb.1010pic.com/questionBank/Upload/2020/11/27/15/1b1ac277/SYS202011271558349761366940_DA/SYS202011271558349761366940_DA.033.png" width="15" height="13" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />��![]() ����
����![]() �ɵ�
�ɵ�![]()
��![]() ����
����![]() �ɵ�
�ɵ�![]()
![]() ��
��![]() ʱ��
ʱ��![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ![]()
�ɢ�֪����![]() ʱ��
ʱ��![]()
��![]() ����
����![]() ����ã�
����ã�![]() ��
��![]() ����ȥ��
����ȥ��
��![]() ����
����![]() �����
�����![]() ��
��![]() ����ȥ��
����ȥ��
![]() k��ȡֵ��ΧΪ��
k��ȡֵ��ΧΪ��![]()
��4�����κ���y��x23x3��m�ֺ���Ϊ
��x23x3��1ʱ��x��1��x��4��
��x2��3x��3��1ʱ��x=![]() ��x��
��x��![]() ��
��
��y��x23x3���߶�ABû�н��㣬m��1��
��y��x23x3���߶�AB��һ�����㣬y��x2��3x��3���߶�AB��һ�����㣬
��![]() ��m��
��m��![]() ��
��
��y��x23x3���߶�AB���������㣬m��4��
����������m��1��![]() ��m��
��m��![]() ��m��4��
��m��4��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
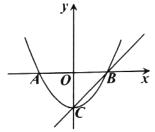
����Ŀ����ͼ����֪����Ϊ![]() ��������
��������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() ��
��
��1�����![]() �����ꣻ
�����ꣻ
��2������κ���![]() �Ľ���ʽ��
�Ľ���ʽ��
��3����ֱ��![]() ����������
����������![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() �������ڣ������
�������ڣ������![]() �����꣺�������ڣ���˵�����ɣ�
�����꣺�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
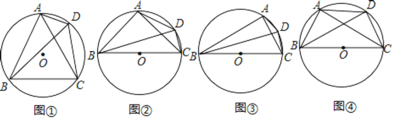
����Ŀ����1������ѡ����ͼ�٣��ı���ABCD�ǡ�O���ڽ��ı��Σ�����AC��BD��AB��BC��AC����֤��BD��AD+CD��
Сӱ��Ϊ���ýس���֤������DB�Ͻ�ȡDM��AD������AM��
С����Ϊ���ò��̷�֤�����ӳ�CD����N��ʹ��DN��AD��
����ѡ��һ�ַ���֤����
��2�����̽������̽��1����ͼ�ڣ��ı���ABCD�ǡ�O���ڽ��ı��Σ�����AC��BD��BC�ǡ�O��ֱ����AB��AC�����õ�ʽ��ʾ�߶�AD��BD��CD֮���������ϵ����֤����Ľ��ۣ�
��̽��2����ͼ�ۣ��ı���ABCD�ǡ�O���ڽ��ı��Σ�����AC��BD����BC�ǡ�O��ֱ������ABC��30�������߶�AD��BD��CD֮��ĵ�����ϵʽ���� ����
��3����չ���룺��ͼ�ܣ��ı���ABCD�ǡ�O���ڽ��ı��Σ�����AC��BD����BC�ǡ�O��ֱ����BC��AC��AB��a��b��c�����߶�AD��BD��CD֮��ĵ�����ϵʽ���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
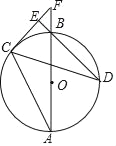
����Ŀ����ͼ��ABΪ��O��ֱ����C��DΪ��O�ϲ�ͬ��A��B�����㣬��ABD��2��BAC������CD������C��CE��DB������ΪE��ֱ��AB��CE���ӳ����ཻ��F�㣮
��1����֤��CF�ǡ�O�����ߣ�
��2����BD��![]() ��sinF��
��sinF��![]() ʱ����OF�ij���
ʱ����OF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���![]() �У���
�У���![]() �͵�
�͵�![]() �ǶԽ���
�ǶԽ���![]() �ϵ����㣬
�ϵ����㣬![]()
![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��

��1����֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��2����![]() ��
��![]() ��BC=4
��BC=4![]() ����
����![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������y=x��ͼ���뷴��������![]() ��ͼ����һ���������������2����
��ͼ����һ���������������2����
��1��x=��3ʱ������������ֵ��
��2������3��x����1ʱ����������y��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2����2m+1��x+m2��4=0����������ȵ�ʵ����
��1����ʵ��m��ȡֵ��Χ��
��2��������ʵ������ƽ���͵���15����ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
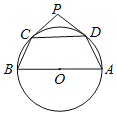
����Ŀ����ͼ��AB�ǡ�O��ֱ����C��DΪ��O�ϵĵ㣬PΪԲ��һ�㣬PC��PD����Բ���У����A+��B��130�㣬��CPD������������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�DZ߳�Ϊ4�ĵȱ������Σ���AB������OM�ϣ���OA��6����D������OM�ϵĶ��㣬����D�����A�غ�ʱ������ACD�Ƶ�C��ʱ�뷽����ת60��õ���BCE������DE����OD��m��
(1)���ⷢ��
��ͼ1����CDE����״���� �������Σ�
(2)̽��֤��
��ͼ2����6��m��10ʱ����BDE���ܳ��Ƿ������Сֵ�������ڣ������BDE�ܳ�����Сֵ���������ڣ���˵�����ɣ�
(3)�������
�Ƿ����m��ֵ��ʹ��DEB��ֱ�������Σ������ڣ���ֱ��д��m��ֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com