
【题目】已知:PA是![]() 的切线,点B在
的切线,点B在![]() 上,连接OB,OP,连接AB交OP于点C,
上,连接OB,OP,连接AB交OP于点C,![]() .
.
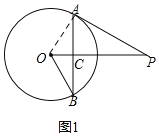
![]() 如图1,求证:
如图1,求证:![]() ;
;
![]() 如图2,OP交
如图2,OP交![]() 于点D,过点D作
于点D,过点D作![]() 交AB于点E,连接OE,求证:
交AB于点E,连接OE,求证:![]() ;
;
![]() 如图3,在
如图3,在![]() 的条件下,延长PO交
的条件下,延长PO交![]() 于点N,连接AN交DF于点M,连接OM、EP,若
于点N,连接AN交DF于点M,连接OM、EP,若![]() ,
,![]() ,求线段BE的长.
,求线段BE的长.

【答案】![]() 证明见解析;
证明见解析;![]() 证明见解析;(3)
证明见解析;(3)![]() .
.
【解析】
![]() 连接OA,由切线性质证
连接OA,由切线性质证![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,根据垂径定理得
,根据垂径定理得![]() ;(2)连接OA交DF于点G,先证
;(2)连接OA交DF于点G,先证![]() ≌
≌![]() 得
得![]() ,再证
,再证![]() ≌
≌![]() 得
得![]() ,所以,
,所以,![]() ,
,![]() ,可证
,可证![]() ;(3)连接AO、AD,作
;(3)连接AO、AD,作![]() 于点L,设
于点L,设![]() ,则
,则![]() ,证
,证![]() ,
,![]() ,
,![]() ,证
,证![]() ≌
≌![]() 得
得![]() ,由中位线性质得
,由中位线性质得![]() ,再证
,再证![]() ≌
≌![]() 得
得![]() ,
,![]() ,再证
,再证![]() ,由
,由![]() ,得
,得![]() ,求出
,求出![]() ,
,![]() ,可得
,可得![]() ,所以,
,所以,![]() ,在
,在![]() 中,设
中,设![]() ,
,![]() ,由勾股定理可知:
,由勾股定理可知:![]() ,可进一步求得
,可进一步求得![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
![]() 连接OA,
连接OA,
![]()
![]()
![]() 是
是![]() 的切线,
的切线,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 连接OA交DF于点G,
连接OA交DF于点G,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
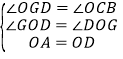 ,
,
![]() ≌
≌![]()
![]() ,
,
在![]() 与
与![]()
![]()
![]() ≌
≌![]()
![]() ,
,
![]() ,
,![]()
![]() .
.

![]() 连接AO、AD,作
连接AO、AD,作![]() 于点L
于点L
设![]() ,则
,则![]() ,
,
![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的直径,
的直径,
![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ≌
≌![]()
![]() ,
,
![]() 为AN的中点,O为ND的中点,
为AN的中点,O为ND的中点,
![]() 为
为![]() 的中位线,
的中位线,
![]() ,
,
在![]() 和
和![]() 中,
中,
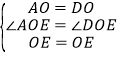
![]() ≌
≌![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() ,
,
![]() ,
,
在![]() 中,
中,
设![]() ,
,![]() ,
,
由勾股定理可知:![]()
解得:![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元.
普通间(元/人/天) | 豪华间(元/人/天) | 贵宾间(元/人/天) | |
三人间 | 50 | 100 | 500 |
双人间 | 70 | 150 | 800 |
单人间 | 100 | 200 | 1500 |
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了 人,一天一共花去住宿费用y元表示,写出y与x的函数关系式;
(3)如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
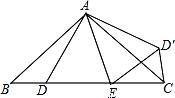
【题目】如图,在△ABC中,AB=AC,D、E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′;
(1)求证:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a﹣b+c≥0;
④ ![]() 的最小值为3.
的最小值为3.
其中,正确结论的个数为( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
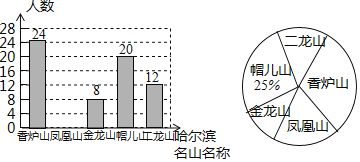
【题目】为贯彻落实十九大会议精神,践行“绿水青山就是金山银山”的发展理念,积极推动生态文明理念融入学校教育,某中学拟举办“爱家乡、览名山”活动,围绕“哈尔滨市周边五大名山,即:香炉山、凤凰山、金龙山、帽儿山、二龙山,你最喜欢那一座山?![]() 每名学生必选且只选一座山
每名学生必选且只选一座山![]() ”的问题在全校范围内随机抽取了部分学生进行问卷调查,根据调查结果绘制了如图所示的不完整统计图
”的问题在全校范围内随机抽取了部分学生进行问卷调查,根据调查结果绘制了如图所示的不完整统计图![]() 请根据统计图的信息回答下列问题:
请根据统计图的信息回答下列问题:
![]() 本次调查共抽取了多少名学生?
本次调查共抽取了多少名学生?
![]() 求本次调查中,最喜欢风凰山的学生人数,并补全条形统计图;
求本次调查中,最喜欢风凰山的学生人数,并补全条形统计图;
![]() 若该中学共有学生1200人,请你估计该中学最喜欢香炉山的学生约有多少人.
若该中学共有学生1200人,请你估计该中学最喜欢香炉山的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程交由甲、乙两个工程队来完成,已知甲工程队单独完成需要60天,乙工程队单独完成需要40天
(1)若甲工程队先做30天后,剩余由乙工程队来完成,还需要用时 天
(2)若甲工程队先做20天,乙工程队再参加,两个工程队一起来完成剩余的工程,求共需多少天完成该工程任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知一次函数![]() 的图象与过
的图象与过![]() 、
、![]() 的直线交于点P,与x轴、y轴分别相交于点C和点D.
的直线交于点P,与x轴、y轴分别相交于点C和点D.
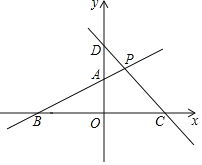
![]() 求直线AB的解析式及点P的坐标;
求直线AB的解析式及点P的坐标;
![]() 连接AC,求
连接AC,求![]() 的面积;
的面积;
![]() 设点E在x轴上,且与C、D构成等腰三角形,请直接写出点E的坐标.
设点E在x轴上,且与C、D构成等腰三角形,请直接写出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:
①∠1=∠2=22.5°;
②点C到EF的距离是 ![]() -1;
-1;
③△ECF的周长为2;
④BE+DF>EF.
其中正确的结论是 . (写出所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数![]() 的图象
的图象![]() 是第一、三象限的角平分线.
是第一、三象限的角平分线.
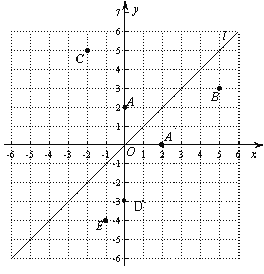
实验与探究:由图观察易知A(0,2)关于直线![]() 的对称点A′的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线
的对称点A′的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线![]() 的对称点B′、C′的位置,并写出它们的坐标: B′____________、C′___________;
的对称点B′、C′的位置,并写出它们的坐标: B′____________、C′___________;
归纳与发现:结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第一、三象限的角平分线![]() 的对称点
的对称点![]() 的坐标为____________;
的坐标为____________;
运用与拓广:已知两点D(0,-3)、E(-1,-4),试在直线![]() 上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com