
 如图,△ABC内接于⊙O,AB为⊙O的直径,∠CBA的平分线交⊙O于点D,DE⊥AB于点E,且交AC于点P,连接AD.
如图,△ABC内接于⊙O,AB为⊙O的直径,∠CBA的平分线交⊙O于点D,DE⊥AB于点E,且交AC于点P,连接AD.分析 (1)先证明△ADE和△ADB均为直角三角形,然后依据同角的余角相等可证明∠ADE=∠ABD,然后结合角平分线的定义以及同弧所对的圆周角相等进行证明即可;
(2)先依据勾股定理求得BD的长,然后在△ADB中依据面积法可求得DE的长,接下来,在△ADE中,依据勾股定理求得AE的长,设PD=PA=x,在△APE中,依据勾股定理列方程求解即可.
解答 解:(1)∵AB是圆O的直径,
∴∠ADB=90°.
∴∠DAB+∠ABD=90°.
∵DE⊥AB,
∴∠AED=90°,
∴∠ADE+∠DAE=90°.
∴∠ADE=∠ABD.
∵BD平分∠CBA,
∴∠ABD=∠CBD.
∴∠ADE=∠CBD.
又∵∠CBD=∠DAC,
∴∠ADE=∠CAD.
(2)∵圆O的半径为5,
∴AB=10.
在△ABD中,由勾股定理得:BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=8.
∵S△ADB=$\frac{1}{2}AD•DB$=$\frac{1}{2}AB•DE$,
∴AD•DB=AB•DE,即10DE=48.
解得:DE=4.8.
在△ADE中,由勾股定理得:AE=$\sqrt{A{D}^{2}-D{E}^{2}}$=3.6.
∵∠ADE=∠CAD,
∴PD=PA.
设PD=PA=x,则PE=4.8-x.
在△APE中,由勾股定理得:AP2=PE2+AE2,即x2=(4.8-x)2+3.62.整理得:9.6x=36,
解得:x=3.75.
∴DP=3.75.
点评 本题主要考查的是圆周角定理、勾股定理、以及等腰三角形的判定、直角三角形两锐角互余的性质,依据勾股定理列出关于x的方程是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 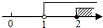 | B. | 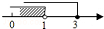 | C. |  | D. | 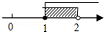 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (5,3) | B. | (5,-1) | C. | (-1,2) | D. | (2,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对旅客上飞机前的安检 | |
| B. | 了解全班同学每周体育锻炼的时间 | |
| C. | 调查奥运会金牌获得者的兴奋剂使用情况 | |
| D. | 调查我国居民对汽车废气污染环境的看法 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com