
【题目】如图所示,已知抛物线y=ax2+bx+c(a≠0)经过点A(﹣2,0)、B(4,0)、C(0,﹣8),与直线y=x﹣4交于B,D两点
(1)求抛物线的解析式并直接写出D点的坐标;
(2)点P为直线BD下方抛物线上的一个动点,试求出△BDP面积的最大值及此时点P的坐标;
(3)点Q是线段BD上异于B、D的动点,过点Q作QF⊥x轴于点F,交抛物线于点G,当△QDG为直角三角形时,直接写出点Q的坐标.

【答案】(1)y=(x+2)(x﹣4),D的坐标是(﹣1,﹣5);(2)P(![]() ,﹣
,﹣![]() );(3)点Q的坐标为(2,﹣2)或(3,﹣1).
);(3)点Q的坐标为(2,﹣2)或(3,﹣1).
【解析】
(1)设抛物线的解析式为y=a(x+2)(x﹣4),将点C的坐标代入可求得a的值,然后将y=x﹣4与抛物线的解析式联立方程组并求解即可;
(2)过点P作PE∥y轴,交直线AB与点E,设P(x,x2﹣2x﹣8),则E(x,x﹣4),则PE═﹣x2+3x+4,然后依据S△BDP=S△DPE+S△BPE,列出△BDP的面积与x的函数关系式,然后依据二次函数的性质求解即可;
(3)设直线y=x﹣4与y轴相交于点K,则K(0,﹣4),设G点坐标为(x,x2﹣2x﹣8),点Q点坐标为(x,x﹣4),先证明△QDG为等腰直角三角形,然后根据∠QDG=90°和∠DGQ=90°两种情况求解即可.
解:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴的交点坐标是A(﹣2,0)、B(4,0),
∴设该抛物线解析式为y=a(x+2)(x﹣4),
将点C(0,﹣8)代入函数解析式代入,得a(0+2)(0﹣4)=﹣8,
解得a=1,
∴该抛物线的解析式为:y=(x+2)(x﹣4)或y=x2﹣2x﹣8.
联立方程组:![]() ,
,
解得![]() (舍去)或
(舍去)或![]() ,
,
即点D的坐标是(﹣1,﹣5);
(2)如图所示:

过点P作PE∥y轴,交直线AB与点E,设P(x,x2﹣2x﹣8),则E(x,x﹣4).
∴PE=x﹣4﹣(x2﹣2x﹣8)=﹣x2+3x+4.
∴S△BDP=S△DPE+S△BPE=![]() PE(xp﹣xD)+
PE(xp﹣xD)+![]() PE(xB﹣xE)=
PE(xB﹣xE)=![]() PE(xB﹣xD)=
PE(xB﹣xD)=![]() (﹣x2+3x+4)=﹣
(﹣x2+3x+4)=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() .
.
∴当x=![]() 时,△BDP的面积的最大值为
时,△BDP的面积的最大值为![]() .
.
∴P(![]() ,﹣
,﹣![]() ).
).
(3)设直线y=x﹣4与y轴相交于点K,则K(0,﹣4),设G点坐标为(x,x2﹣2x﹣8),点Q点坐标为(x,x﹣4).
∵B(4,0),
∴OB=OK=4.
∴∠OKB=∠OBK=45°.
∵QF⊥x轴,
∴∠DQG=45°.
若△QDG为直角三角形,则△QDG是等腰直角三角形.
①当∠QDG=90°时,过点D作DH⊥QG于H,

∴QG=2DH,QG=﹣x2+3x+4,DH=x+1,
∴﹣x2+3x+4=2(x+1),解得:x=﹣1(舍去)或x=2,
∴Q1(2,﹣2).
②当∠DGQ=90°,则DH=QH.
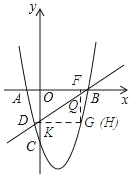
∴﹣x2+3x+4=x+1,解得x=﹣1(舍去)或x=3,
∴Q2(3,﹣1).
综上所述,当△QDG为直角三角形时,点Q的坐标为(2,﹣2)或(3,﹣1).


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】书店老板去图书批发市场购买某种图书,第一次用 1200 元购买若干本,按 每本 10 元出售,很快售完.第二次购买时,每本书的进价比第一次提高了 20%,他用1500 元所购买的数量比第一次多 10 本.
(1)求第一次购买的图书,每本进价多少元?
(2)第二次购买的图书,按每本 10 元售出 200 本时,出现滞销,剩下的图书降价后全部 售出,要使这两次销售的总利润不低于 2100 元,每本至多降价多少元?(利润=销售收入一进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=x2+bx+c(a≠0)的图象经过点A(1,0)且与y轴交卡点C,点B和点C关于该二次函数图象的对称轴直线x=2对称,一次函数y=kx+b的图象经过点A及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,直接写出不等式kx+b≤x2+bx+c的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组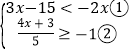
请结合题意填空,完成本题的解答.
(1)解不等式①,得________;
(2)解不等式②,得________;
(3)把不等式①和②的解集在数轴上表示出来;
![]()
(4)原不等式组的解集为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com