
【题目】在平面直角坐标系xOy中,抛物线y=ax2-4ax+c(a≠0)与y轴交于点A,将点A向右平移2个单位长度,得到点B.直线![]() 与x轴,y轴分别交于点C,D.
与x轴,y轴分别交于点C,D.
(1)求抛物线的对称轴.
(2)若点A与点D关于x轴对称.
①求点B的坐标.
②若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
【答案】(1)x=2;(2)点B坐标为(2,3);②a>0或a≤![]() .
.
【解析】
(1)根据二次函数y=ax2+bx+c(a≠0)的对称轴方程为x=![]() 即可的答案;
即可的答案;
(2)①根据直线![]() 与x轴,y轴分别交于点C,D可得C、D两点坐标,根据关于x轴对称的点的坐标特征可得A点坐标,根据平移性质即可得B点坐标;
与x轴,y轴分别交于点C,D可得C、D两点坐标,根据关于x轴对称的点的坐标特征可得A点坐标,根据平移性质即可得B点坐标;
②分a>0与a<0两种情况,结合图象,根据二次函数的性质即可得答案.
(1)∵抛物线的解析式为y=ax2-4ax+c(a≠0),
∴抛物线的对称轴为x=![]() =2,
=2,
(2)①∵直线解析式为![]() ,
,
∴x=0时,y=-3,y=0时,x=5,
∴C点坐标为(5,0),D点坐标为(0,-3),
∵点A于点D关于x轴对称,
∴点A坐标为(0,3),
∵将点A向右平移2个单位长度,得到点B,
∴点B坐标为(2,3).
②如图,当a>0时,抛物线开口向上,
∵点A(0,3),对称轴为x=2,
∴抛物线经过点A关于x=2的对称点(4,3),
∴抛物线与线段BC都有交点,
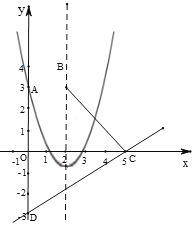
当a<0时,抛物线的开口向下,
∵点A(0,3),
∴c=3,
∴抛物线解析式为y=ax2-4ax+3,
当x=5时,25a-20a+3=0,
解得:a=![]() ,
,
∵![]() 越大,抛物线的开口越小,
越大,抛物线的开口越小,
∴a≤![]() .
.
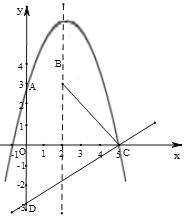
综上所述:a的取值范围为a>0或a≤![]() .
.


科目:初中数学 来源: 题型:
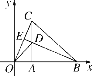
【题目】如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=![]() ,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是________.
,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 上部分点的横坐标x与纵坐标y的对应值如下表
上部分点的横坐标x与纵坐标y的对应值如下表
x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | -4 | 0 | 2 | 2 | 0 | -4 | … |
下列结论:①抛物线开口向下;②当![]() 时,y随x的增大而减小;③抛物线的对称轴是直线
时,y随x的增大而减小;③抛物线的对称轴是直线![]() ;④函数
;④函数![]() 的最大值为2.其中所有正确的结论为( )
的最大值为2.其中所有正确的结论为( )
A.①②③B.①③C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
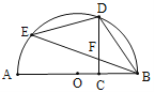
【题目】如图,AB是⊙O的直径,C是线段OB上的一点(不与点B重合),D,E是半圆上的点且CD与BE交于点F,用①![]() ,②DC⊥AB,③FB=FD中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
,②DC⊥AB,③FB=FD中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形中,除直角外的5个元素中,已知2个元素(其中至少有1个是边),就可以求出其余的3个未知元素.对于任意三角形,我们需要知道几个元素就可以求出其余的未知元素呢?思考并解答下列问题:
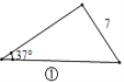
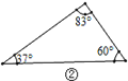
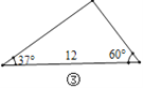
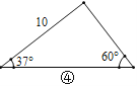
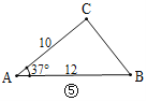
(1)观察图①~图④,根据图中三角形的已知元素,可以求出其余未知元素的序号是____.
(2)如图⑤,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:
,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了解旅游人数的变化情况,收集并整理了2017年1月至2019年12月期间的月接待旅游量(单位:万人次)的数据并绘制了统计图如下:
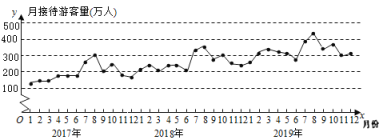
根据统计图提供的信息,下列推断不合理的是( )
A.2017年至2019年,年接待旅游量逐年增加
B.2017年至2019年,各年的月接待旅游量高峰期大致在7,8月份
C.2019年的月接待旅游量的平均值超过300万人次
D.2017年至2019年,各年下半年(7月至12月)的月接待旅游量相对于上半年(1月至6月)波动性更小,变化比较平稳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数![]() 的图象G经过点
的图象G经过点![]() ,直线
,直线![]() 与y轴交于点B,与图象G交于点C.
与y轴交于点B,与图象G交于点C.
(1)求m的值.
(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,C之间的部分与线段BA,BC围成的区域(不含边界)为W.
①当直线l过点![]() 时,直接写出区域W内的整点个数.
时,直接写出区域W内的整点个数.
②若区域W内的整点不少于4个,结合函数图象,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把分别标有数字1,2,3,4的四个小球放入A袋内,把分别标有数字-1,-2,-2,-3,5的五个小球放入B袋内,所有的小球除了标有的数字不同外,其余完全相同.
(1)学生甲从A、B两个袋子中各摸出一个小球,求这两个小球上的数字互为相反数的概率.
(2)当B袋中标有5的小球的数字变为 时,(1)中的概率为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
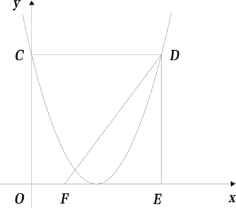
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于点C,过点C作CD∥
轴交于点C,过点C作CD∥![]() 轴交该函数的图象于点D,过点D作DE∥
轴交该函数的图象于点D,过点D作DE∥![]() 轴交
轴交![]() 轴于点E,已知点F(1,0),连接DF.
轴于点E,已知点F(1,0),连接DF.
(1)请求出该函数图象的项点坐标(用含![]() 的代数式表示);
的代数式表示);
(2)如图,若该二次函数的图象的顶点落在![]() 轴上,P为对称轴右侧抛物线上一点;
轴上,P为对称轴右侧抛物线上一点;
①连接PD、PE、PF,若![]() ,求点P的坐标;
,求点P的坐标;
②若∠PFD=![]() ∠DEF,点P的横坐标为m,则m的值为 .
∠DEF,点P的横坐标为m,则m的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com