
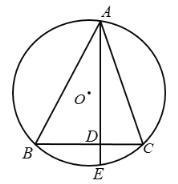
【题目】如图,![]() 是
是![]() 的外接圆,
的外接圆,![]() ,
,![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长是_________.
的长是_________.
【答案】![]()
【解析】
连结OB,OC,OA,过O点作OF⊥BC于F,作OG⊥AE于G,根据圆周角定理可得∠BOC=90°,根据等腰直角三角形的性质和勾股定理可得DG,AG,可求AD,再根据相似三角形的判定和性质可求DE.
解:连结OB,OC,OA,过O点作OF⊥BC于F,作OG⊥AE于G,
∵⊙O是△ABC的外接圆,∠BAC=45°,
∴∠BOC=90°,
∵BD=4,CD=1,
∴BC=4+1=5,
∴OB=OC=![]() ,
,
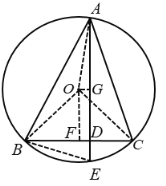
∴OA=![]() ,OF=BF=
,OF=BF=![]() ,
,
∴DF=BDBF=![]() ,
,
∴OG=![]() ,GD=
,GD=![]() ,
,
在Rt△AGO中,AG=![]() ,
,
∴AD=AG+GD=![]() ,
,
∵连接BE,AD与BE相交于D,
∴∠BED=∠ACD,∠BDE=∠ADC,
∴△BDE∽△ADC,
∴![]()
 .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
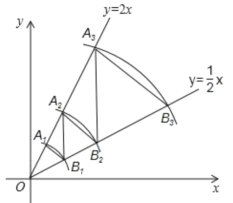
【题目】二次函数![]() 的函数图象如图,点
的函数图象如图,点![]() 位于坐标原点,点
位于坐标原点,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在二次函数
在二次函数![]() 位于第一象限的图象上,
位于第一象限的图象上,![]() ,
,![]() ,
,![]() ,
,![]() …都是直角顶点在抛物线上的等腰直角三角形,则
…都是直角顶点在抛物线上的等腰直角三角形,则![]() 的斜边长为( )
的斜边长为( )

A.20B.![]() C.22D.
C.22D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 长为半径画弧,交直线
长为半径画弧,交直线![]() 于点
于点![]() ,过
,过![]() 点作
点作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,以
,以![]() 为圆心,以
为圆心,以![]() 长为半径画弧,交直线
长为半径画弧,交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 长为半径画弧,交直线
长为半径画弧,交直线![]() 于点
于点![]() ,过
,过![]() 点作
点作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 长为半径面弧,交直线
长为半径面弧,交直线![]() 于点
于点![]() ,…,按照如此规律进行下去,点
,…,按照如此规律进行下去,点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一块长为40cm,宽为30cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为600cm2,设剪去小正方形的边长为xcm,则可列方程为( )
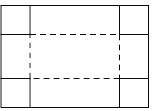
A.(30﹣2x)(40﹣x)=600B.(30﹣x)(40﹣x)=600
C.(30﹣x)(40﹣2x)=600D.(30﹣2x)(40﹣2x)=600
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形![]() 中,点
中,点![]() 为对角线
为对角线![]() 上一动点(点
上一动点(点![]() 与点
与点![]() 、
、![]() 不重合),连接
不重合),连接![]() ,作
,作![]() 交射线
交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() 、
、![]() ,作射线
,作射线![]() 交射线
交射线![]() 于点
于点![]()
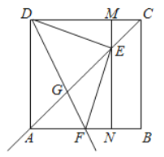
(1)求证:![]() ;
;
(2)当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
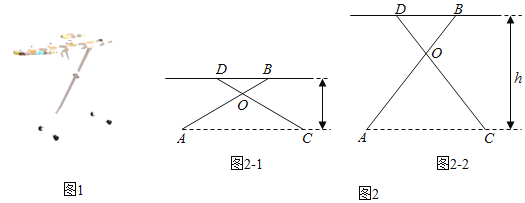
【题目】有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图.AB和CD是两根相同长度的活动支撑杆,点O是它们的连接点,OA=OC,h(cm)表示熨烫台的高度.
(1)如图2﹣1.若AB=CD=110cm,∠AOC=120°,求h的值;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度为120cm时,两根支撑杆的夹角∠AOC是74°(如图2﹣2).求该熨烫台支撑杆AB的长度(结果精确到lcm).
(参考数据:sin37°≈0.6,cos37°≈0.8,sin53°≈0.8,cos53°≈0.6.)
查看答案和解析>>
科目:初中数学 来源: 题型:
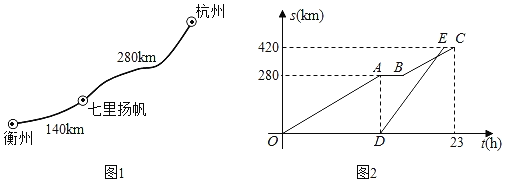
【题目】2020年5月16日,“钱塘江诗路”航道全线开通,一艘游轮从杭州出发前往衢州,线路如图1所示.当游轮到达建德境内的“七里扬帆”景点时,一艘货轮沿着同样的线路从杭州出发前往衢州.已知游轮的速度为20km/h,游轮行驶的时间记为t(h),两艘轮船距离杭州的路程s(km)关于t(h)的图象如图2所示(游轮在停靠前后的行驶速度不变).
(1)写出图2中C点横坐标的实际意义,并求出游轮在“七里扬帆”停靠的时长.
(2)若货轮比游轮早36分钟到达衢州.问:
①货轮出发后几小时追上游轮?
②游轮与货轮何时相距12km?
查看答案和解析>>
科目:初中数学 来源: 题型:
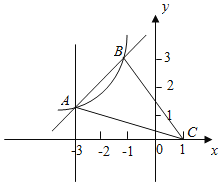
【题目】如图,在平面立角坐标系中,反比例函数y=![]() (k≠0,x<0)与一次函数y=ax+b的图象交于点A(﹣3,1)、B(m,3).点C的坐标为(1,0),连接AC,BC.
(k≠0,x<0)与一次函数y=ax+b的图象交于点A(﹣3,1)、B(m,3).点C的坐标为(1,0),连接AC,BC.
(1)求反比例函数和一次函数的表达式;
(2)当x<0时,直接写出不等式![]() ≥ax+b的解集 ;
≥ax+b的解集 ;
(3)若点M为y轴的正半轴上的动点,当△ACM是直角三角形时,直接写出点M的坐标 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com