
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式先计算乘方及绝对值运算,再计算乘除运算,最后算加减运算即可得到结果;
(3)方程去括号,移项合并,把x系数化为1,即可求出解;
(4)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)原式=14+12-25-17=26-42=-16;
(2)原式=-1-25=-26;
(3)去括号得:2x+5=3x-3,
移项合并得:-x=-8,
解得:x=8;
(4)去分母得:2(2x+1)-(5x-1)=6,
去括号得:4x+2-5x+1=6,
移项合并得:-x=3,
解得:x=-3.
点评 此题考查了解一元一次方程,以及有理数的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:选择题
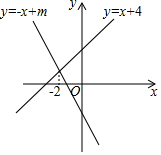 如图,直线y=-x+m与y=x+4的交点的横坐标为-2,则关于x的不等式-x+m>x+4的解集为( )
如图,直线y=-x+m与y=x+4的交点的横坐标为-2,则关于x的不等式-x+m>x+4的解集为( )| A. | x>-2 | B. | x<-2 | C. | x>-4 | D. | x<-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
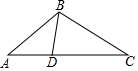 如图,△ABC中,点D在AC边上,添加下列条件后仍不能判别△ABD∽△ACB的是( )
如图,△ABC中,点D在AC边上,添加下列条件后仍不能判别△ABD∽△ACB的是( )| A. | ∠ABD=∠C | B. | ∠ADB=∠ABC | C. | $\frac{AD}{AB}$=$\frac{AB}{AC}$ | D. | $\frac{AD}{AB}$=$\frac{BD}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC
如图,△ABC中,AB=AC查看答案和解析>>
科目:初中数学 来源: 题型:选择题
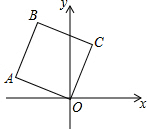 如图,在正方形OABC中,点A的坐标是(-3,1),点B的纵坐标是4,则B,C两点的坐标分别是( )
如图,在正方形OABC中,点A的坐标是(-3,1),点B的纵坐标是4,则B,C两点的坐标分别是( )| A. | (-2,4),(1,3) | B. | (-2,4),(2,3) | C. | (-3,4),(1,4) | D. | (-3,4),(1,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
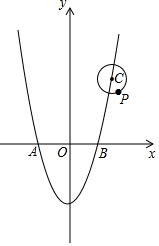 【材料阅读】阅读下列一段文字,然后回答下列问题.
【材料阅读】阅读下列一段文字,然后回答下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com