
分析 (1)根据“灵动数”的特征,列出算式求解即可;
(2)先求出51×52<2700,51×55>2800,根据整数的定义求出51×53,51×54的积,从而求解.
解答 解:(1)724-2×5=714,71-4×5=51,51÷17=3,
所以7242能被17整除,是“灵动数”;
209875-4×5=209855,20985-5×5=20960,2096-0×5=2096,209-6×5=179,179÷17=10…9,
所以209875不能被17整除,不是“灵动数”;
(2)∵51×52<2700,51×55>2800,
51×53=2703,51×54=2754,
∴这个数是2703或2754.
点评 此题主要考查了新定义,数的整除,解本题的关键是理解新定义,掌握数的整除是解本题的难点.


科目:初中数学 来源: 题型:选择题
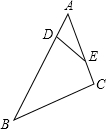 如图,在△ABC中,点D、E分别在AB、AC边上,且AD=2,AE=4,BD=10,CE=2,则DE:BC等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,且AD=2,AE=4,BD=10,CE=2,则DE:BC等于( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 1:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
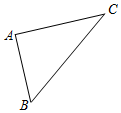 如图,在△ABC中,∠A=90°,sinB=$\frac{4}{5}$,则cosB等于( )
如图,在△ABC中,∠A=90°,sinB=$\frac{4}{5}$,则cosB等于( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
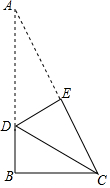 如图,折叠直角三角形ABC纸片,使两锐角顶点A、C重合,设折痕为DE.若AB=4,BC=3,则BD的值是( )
如图,折叠直角三角形ABC纸片,使两锐角顶点A、C重合,设折痕为DE.若AB=4,BC=3,则BD的值是( )| A. | $\frac{7}{8}$ | B. | 1 | C. | $\frac{9}{8}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C,D,E,F,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=6,则EF的值为( )
如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C,D,E,F,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=6,则EF的值为( )| A. | 4 | B. | 6 | C. | 9 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com