
分析 (1)根据判别式的意义得到△=32-4(k-1)≥0,然后解不等式求出满足条件的正整数即可;
(2)把(1)k的中分别代入方程可判断k=3满足条件,当k=3时,方程变形为x2+3x+2=0,解得x1=-1,x2=-2,从而得到A点和B点坐标为(-1,0),(-2,0),再求出C(0,2),
①根据三角形面积公式计算△ABC的面积;
②讨论:当A(-2,0),B(-1,0),C(0,2),利用等腰直角三角形的性质求BH;
当A(-1,0),B(-2,0),C(0,2),则利用面积法求BH.
解答 解:(1)根据题意得△=32-4(k-1)≥0,解得k≤$\frac{13}{4}$,
而k为正整数.
所以k的值为1、2、3、4;
(2)当k=1时,方程变形为x2+3x=0,解得x1=0,x2=-3,
当k=2时,方程变形为x2+3x+1=0,解得x1=$\frac{-3+\sqrt{5}}{2}$,x2=$\frac{-3-\sqrt{5}}{2}$,
当k=4时,方程变形为x2+3x+3=0,方程没有实数解,
当k=3时,方程变形为x2+3x+2=0,解得x1=-1,x2=-2,
此时二次函数为y=x2+3x+2,A点和B点坐标为(-1,0),(-2,0),
当x=0时,y=x2+3x+2=2,则C(0,2),
①△ABC的面积=$\frac{1}{2}$×2×1=1;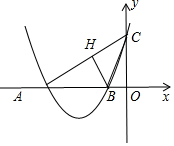
②当A(-2,0),B(-1,0),C(0,2),
∵OC=OA,
∴△OAC为等腰直角三角形,
∴∠BAH=45°,
∴△ABH为等腰直角三角形,
∴BH=$\frac{\sqrt{2}}{2}$AB=$\frac{\sqrt{2}}{2}$,
当A(-1,0),B(-2,0),C(0,2),则AC=$\sqrt{5}$,
∵$\frac{1}{2}$BH•AC=$\frac{1}{2}$•AB•OC,
∴BH=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,
即BH为$\frac{\sqrt{2}}{2}$或$\frac{\sqrt{5}}{5}$.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了三角形面积公式.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
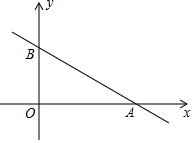 如图,在平面直角坐标系内A(8,0),B(0,6),若直线L与AB平行,且在直线L上有且只有一点P使∠OPA=90°,求满足条件的直线L的解析式.
如图,在平面直角坐标系内A(8,0),B(0,6),若直线L与AB平行,且在直线L上有且只有一点P使∠OPA=90°,求满足条件的直线L的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
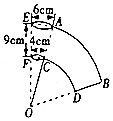 如图所示是一个纸杯,它的母线延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6cm,下底面直径为4cm,母线长EF=9cm,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π)
如图所示是一个纸杯,它的母线延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6cm,下底面直径为4cm,母线长EF=9cm,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
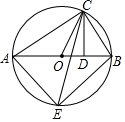 如图,Rt△ABC内接于⊙O,∠ACB=90°,CD⊥AB于点D,CE平分∠OCD.
如图,Rt△ABC内接于⊙O,∠ACB=90°,CD⊥AB于点D,CE平分∠OCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com