
����Ŀ�������̳����������ij�ֹ���Ʒʱ��ÿ���ɻ���45Ԫ������۵İ��������۸ù���Ʒ8���뽫��۽���35Ԫ���۸ù���Ʒ12������������ȣ�
��1���ù���Ʒÿ���Ľ��ۡ���۷ֱ��Ƕ���Ԫ��
��2����ÿ������Ʒ����1������õĽ��۽���������۳��������̳�ÿ����۳��ù���Ʒ100������ÿ������Ʒ����1Ԫ����ÿ��ɶ��۳��ù���Ʒ4������ÿ������Ʒ���۶���Ԫ���ۣ�ÿ���õ��������õ���������Ƕ���Ԫ��
���𰸡���1��155��200��2����ÿ��Ӧ����10Ԫ���ۣ�ÿ���õ�����������������4900Ԫ
�������������������1����ù���Ʒÿ���Ľ�����xԪ�������yԪ�����������г������飬������ɣ���2����ÿ��Ӧ����aԪ���ۣ�ÿ���õ�����ΪWԪ�����������г�������ϵʽ�����䷽�������ֵ����.
���������
��1����ù���Ʒÿ���Ľ�����xԪ�������yԪ��������÷����飺
![]()
��ã� ![]() ��
��
�ʸù���Ʒÿ���Ľ�����155Ԫ�������200Ԫ��
��2����ÿ��Ӧ����aԪ���ۣ�ÿ���õ�����ΪWԪ��
������ɵ�W��a�ĺ�����ϵʽ��W=��45��a����
W=��4a2+80a+4500��
�䷽�ã�W=��4��a��10��2+4900��
��a=10ʱ��W���=4900��
��ÿ��Ӧ����10Ԫ���ۣ�ÿ���õ�����������������4900Ԫ��


 �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д� ˫��ͬ������ѵ��ϵ�д�
˫��ͬ������ѵ��ϵ�д� �Ƹ�С״Ԫͬ������������ϵ�д�
�Ƹ�С״Ԫͬ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AC=a��BD=b����AC��BD��˳�������ı���ABCD�����е㣬�õ��ı���A1B1C1D1 �� ��˳�������ı���A1B1C1D1�����е㣬�õ��ı���A2B2C2D2 �� ��˽�����ȥ���õ��ı���AnBnCnDn �� 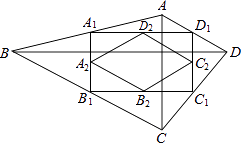
��1����֤���ı���A1B1C1D1�Ǿ��Σ�
��2���ı���A3B3C3D3���Σ�
��3���ı���A1B1C1D1���ܳ�Ϊ��
��4���ı���AnBnCnDn�����Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���Ӷ��κ���y=ax2+bx+c��ͼ����ͼ���й۲�ó�������������Ϣ����c��0����abc��0����a��b+c��0����2a��3b=0����c��4b��0������Ϊ������ȷ����Ϣ�ǣ�������

A. �٢ڢۢ� B. �٢ڢۢ� C. �٢ۢܢ� D. �ڢۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һԪ���η���3x2��1=4x����һ����ʽΪ�� ��
A.3x2+4x=1
B.3x2��4x=1
C.3x2��4x��1=0
D.3x2+4x��1=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
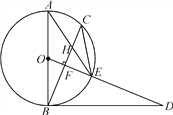
����Ŀ����ͼ��AB�ǡ�O��ֱ������CΪ��O��һ�㣬OF��BC�ڵ�F������O�ڵ�E��AE��BC���ڵ�H����DΪOE���ӳ�����һ�㣬�ҡ�ODB����AEC.
��֤����1��BD�ǡ�O�����ߣ�
��2����EH=2,AH=6,��CE�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD��BC��D��EG��BC��G����E=��1����˵��ADƽ�֡�BAC�����ɣ� 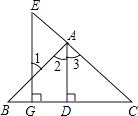
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ڡ�ABC������һ��P��x0 �� y0������ƽ�ƺ��Ӧ��ΪP1��x0+3��y0��3��������ABC��ͬ��ƽ�Ƶõ���DEF�� 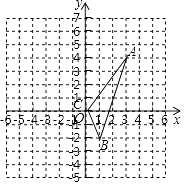
��1�����ABC�������
��2����д��D��E��F�����꣬����ͼ�л�����DEF��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com