
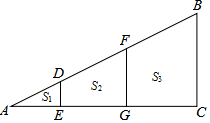
 如图,△ABC中,D,F是边AB上两点,DE∥FG∥BC,DF=FB,△ADE的面积为S1,四边形DFGE和四边形FBCG的面积分别为S2,S3.
如图,△ABC中,D,F是边AB上两点,DE∥FG∥BC,DF=FB,△ADE的面积为S1,四边形DFGE和四边形FBCG的面积分别为S2,S3.分析 (1)先求出S1+S2的面积,由于DE∥FG∥BC,所以△ADE∽△AFG,$\frac{A{D}^{2}}{A{F}^{2}}$=$\frac{{S}_{1}}{{S}_{1}+{S}_{2}}$,从而可求出$\frac{AD}{AF}$的值,再根据DF=FB,即可得出$\frac{AD}{AB}$的值,从而可求出S3
(2)设S1=x,然后根据(1)中的结论即可求出x的值.
解答 解:(1)∵DE∥FG,
∴△ADE∽△AFG,
∴$\frac{A{D}^{2}}{A{F}^{2}}$=$\frac{{S}_{1}}{{S}_{1}+{S}_{2}}$=$\frac{1}{9}$
∴$\frac{AD}{AF}=\frac{1}{3}$,
∵DF=FB,
∴$\frac{AD}{AB}=\frac{1}{5}$,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{A{D}^{2}}{A{B}^{2}}$=$\frac{{S}_{1}}{{S}_{1}+{S}_{2}+{S}_{3}}$
∴S3=16,
(2)设S1=x,
由(1)可知:$\frac{A{D}^{2}}{A{F}^{2}}$=$\frac{x}{2+x}$
∴$\frac{AD}{AF}=\frac{\sqrt{x}}{\sqrt{2+x}}$,
∵DF=FB,
∴$\frac{AD}{AB}$=$\frac{\sqrt{x}}{2\sqrt{2+x}-\sqrt{x}}$,
∵$\frac{A{D}^{2}}{A{B}^{2}}$=$\frac{{S}_{1}}{{S}_{1}+{S}_{2}+{S}_{3}}$
∴$\frac{x}{x+5}$=($\frac{\sqrt{x}}{2\sqrt{2+x}-\sqrt{x}}$)2
解得:x=$\frac{9}{8}$
故答案为:(1)16;(2)$\frac{9}{8}$
点评 本题考查相似三角形的性质,解题的关键是正确运用相似三角形的面积比等于相似比的平方,本题属于中等题型.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,?ABCD的一边BC在x轴上,OC=2,点D的坐标为(-3,3),BC=4.
如图,在平面直角坐标系中,?ABCD的一边BC在x轴上,OC=2,点D的坐标为(-3,3),BC=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
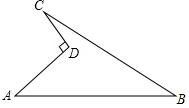 如图是校园内的一块菜地,数学活动小组的同学量得:∠ADC=90°,AD=40m,CD=30m,BC=120m,AB=130m,求这块菜地的面积.
如图是校园内的一块菜地,数学活动小组的同学量得:∠ADC=90°,AD=40m,CD=30m,BC=120m,AB=130m,求这块菜地的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
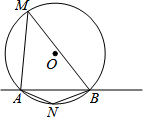 如图,⊙O的半径是4,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
如图,⊙O的半径是4,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )| A. | $4\sqrt{2}$ | B. | $8\sqrt{2}$ | C. | $12\sqrt{2}$ | D. | $16\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
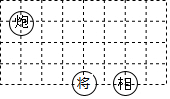 如图,若在象棋盘上建立平面直角坐标系,使“将”位于点(-1,-2),“相”位于(1,-2),则“炮”位于点( )
如图,若在象棋盘上建立平面直角坐标系,使“将”位于点(-1,-2),“相”位于(1,-2),则“炮”位于点( )| A. | (1,4) | B. | (4,1) | C. | (-4,1) | D. | (1,-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com