
【题目】某文具用品商店销售A、B两种款式文具盒,已知购进1个A款文具盒比B款文具盒便宜5元,且用300元购入A款文具盒的数量比购入B款文具盒的数量多5个.
(1)购进一个A款文具盒、一个B款文具盒各需多少元?
(2)若A款文具盒与B款文具盒的售价分别是20元和30元,现该文具用品商店计一划用不超过1000元购入共计60个A、B两种款式的文具盒,且全部售完,问如何安排进货才能使销售利润最大?并求出最大利润.
【答案】(1)购进一个A款文具盒、一个B款文具盒分别需要15元和20元;(2)最大利润为400元.
【解析】(1)设购进一个A款文具盒需x元,则一个B款文具盒需(x+5)元,根据用300元购入A款文具盒的数量比购入B款文具盒的数量多5列出方程,求出方程的解即可得到结果;
(2)设该商店购进A款文具盒a个,则购进B款文具盒(60﹣a)个,所获的利润为W元,列出W关于x的关系式,且列出a的不等式,利用一次函数的性质确定出获得的最大利润即可.
(1)设购进一个A款文具盒需x元,则一个B款文具盒需(x+5)元,根据题意,得:
![]() ﹣
﹣![]() =5,
=5,
解得:x1=15,x2=﹣20,
经检验,x=15是原方程的根,也符合题意.
答:购进一个A款文具盒需15元,一个B款文具盒需20元.
(2)设该商店购进A款文具盒a个,则购进B款文具盒(60﹣a)个,所获的利润为W元,根据题意,得:
W=(20﹣15)a+(30﹣20)(60﹣a)=﹣5a+600.
∵该文具用品商店计划用不超过1000元购入共计60个A、B两种款式的文具盒,∴15a+20(60﹣a)≤1000,∴a≥40.
∵k=﹣5<0,∴W随a的增大而减小,当a=40时,W有最大值,为﹣5×40+600=400,则获得最大利润为400元.


科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AB、AC为腰分别向外作等腰直角三角形ABD和等腰直角三角形ACE,连接DE.若M为BC中点,MA延长线交DE于点H,
(1) 求证:AH⊥DE.
(2) 若DE=4,AH=3,求△ABM的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=45°.若AD平分∠BAC交BC于D,BE⊥AC于E,且交A于O,连接OC.则下列说法中正确的是( )①AD⊥BC;②OC平分BE;③OE=CE;④△ACD≌△BCE;⑤△OCE的周长=AC的长度

A.①②③B.②④⑤C.①③⑤D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
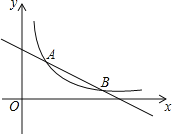
【题目】如图,已知反比例函数y=![]() (x>0)的图象与一次函数y=﹣
(x>0)的图象与一次函数y=﹣![]() x+4的图象交于A和B(6,n)两点.
x+4的图象交于A和B(6,n)两点.
(1)求k和n的值;
(2)若点C(x,y)也在反比例函数y=![]() (x>0)的图象上,求当2≤x≤6时,函数值y的取值范围.
(x>0)的图象上,求当2≤x≤6时,函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,直线AB与![]() 轴交于点A(-2,0),与
轴交于点A(-2,0),与![]() 轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线
轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线![]() 上,则
上,则![]() 的值( )
的值( )

A. -4 B. -2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
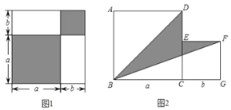
【题目】请认真观察图形,解答下列问题:
(1)根据图1中条件,试用两种不同方法表示两个阴影图形的面积的和.
方法1: .
方法2: .
(2)从中你能发现什么结论?请用等式表示出来: .
(3)利用(2)中结论解决下面的问题:如图2,两个正方形边长分别为a、b,如果a+b=10,ab=21,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD边上的一动点,它从点A出发沿在A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
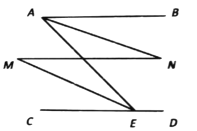
【题目】已知如图,![]() ,
,![]() .
.
求证:![]()
证明:因为![]() (已知)
(已知)
所以![]() (_______)
(_______)
所以![]() __________.(两直线平行,内错角相等)
__________.(两直线平行,内错角相等)
因为![]() .(已知)
.(已知)
所以![]() __________.(_______)
__________.(_______)
所以![]() .(_______)
.(_______)
所以![]() .(等式性质1)
.(等式性质1)
即![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com