
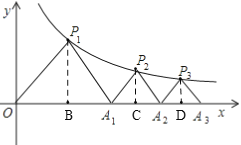
【题目】如图,△P1OA1,△P2A1A2,△P3A2A3,…,是等腰直角三角形,点P1,P2,P3,…,在反比例函数y=![]() 的图象上,斜边OA1,A1A2,A2A3,…都在x轴上,则点A3的坐标是_____.
的图象上,斜边OA1,A1A2,A2A3,…都在x轴上,则点A3的坐标是_____.

【答案】(4![]() ,0)
,0)
【解析】
如图,过点P1作P1B⊥x轴,过点P2作P1C⊥x轴,过点P3作P3D⊥x轴,由于△OA1P1是等腰直角三角形可得P1B=OB=![]() OA1,所以设P1点的坐标是(a,a),把(a,a)代入y=
OA1,所以设P1点的坐标是(a,a),把(a,a)代入y=![]() 可求出a=2,可得B的坐标是(2,0),进一步得到OA1=4,再根据△P2A1A2是等腰直角三角形,设P2的纵坐标是b,可知P2横坐标是b+4,把P2的坐标代入解析式y=
可求出a=2,可得B的坐标是(2,0),进一步得到OA1=4,再根据△P2A1A2是等腰直角三角形,设P2的纵坐标是b,可知P2横坐标是b+4,把P2的坐标代入解析式y=![]() ,即可求出b,然后即可求出点C的坐标,进而得出A2坐标,同理即可得A3坐标.
,即可求出b,然后即可求出点C的坐标,进而得出A2坐标,同理即可得A3坐标.
如图,过点P1作P1B⊥x轴,过点P2作P1C⊥x轴,过点P3作P3D⊥x轴,
∵△OA1P1是等腰直角三角形,
∴P1B=OB=![]() OA1,
OA1,
∴设P1坐标为(a,a),
∵P1在反比例函数y=![]() 图象上,
图象上,
∴![]() ,
,
解得:a=2,(负值舍去)
∴B点坐标为(2,0),
∴OA1=4,
设P2的纵坐标为b,
∵△P2A1A2是等腰直角三角形,
∴P2C=A1C=![]() A1A2,
A1A2,
∴横坐标为4+b,
∵P2在反比例函数y=![]() 图象上,
图象上,
∴![]() ,
,
解得:b=![]() ,(负值舍去)
,(负值舍去)
∴A1A2=2 P2C=![]() ,
,
∴OA2=OA1+A1A2=![]() ,
,
同理,设P3坐标为(![]() +c,c),
+c,c),
∴![]() ,
,
解得:c=![]() ,(负值舍去)
,(负值舍去)
∴OA3=![]() +2×(
+2×(![]() )=
)=![]() ,
,
∴A3的坐标为(![]() ,0),
,0),
故答案为:(![]() ,0)
,0)


 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】下列图形都是由大小相同的黑点按一定规律组成的,第①个图形中有3个黑点第②个图形中有11个黑点,第③个图形中有27个黑点,…,按此规律排列,则第⑦个图形中黑点的个数为( )

A.123B.171C.172D.180
查看答案和解析>>
科目:初中数学 来源: 题型:
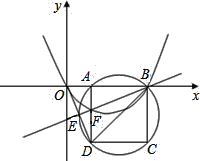
【题目】如图,在平面直角坐标系中,已知点![]() 、
、![]() ,以
,以![]() 为边在
为边在![]() 轴下方作正方形
轴下方作正方形![]() ,点
,点![]() 是线段
是线段![]() 与正方形
与正方形![]() 的外接圆的交点,连接
的外接圆的交点,连接![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,试求经过
,试求经过![]() 、
、![]() 、
、![]() 三点的抛物线
三点的抛物线![]() 的解析式;
的解析式;
(3)在(2)的条件下,将抛物线![]() 在
在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折,图象的其余部分保持不变,得到一个新图象,若直线
轴翻折,图象的其余部分保持不变,得到一个新图象,若直线![]() 向上平移t个单位与新图象有两个公共点,试求t的取值范围.
向上平移t个单位与新图象有两个公共点,试求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
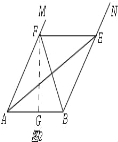
【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DE上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.
(1)求sin∠EAC的值.
(2)求线段AH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
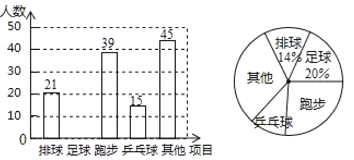
【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项.现随机抽查了部分学生,并将其结果绘制成如下不完整的条形图和扇形图.
抽取的学生最喜欢体育活动的条形统计图
抽取的学生最喜欢体育活动的扇形统计图
请结合以上信息解答下列问题:
(1)在这次调查中一共抽查了_____学生,扇形统计图中“乒乓球”所对应的圆心角为_____度,并请补全条形统计图;
(2)己知该校共有1200名学生,请你估计该校最喜爱跑步的学生人数;
(3)若在“排球、足球、跑步、乒乓球”四个活动项目任选两项设立课外兴趣小组,请用列表法或画树状图的方法求恰好选中“排球、乒乓球”这两项活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成一件事有几类办法,各类办法相互独立,每类办法中又有多种不同的办法,则完成这件事的不同办法数是各类不同方法种数的和,这就是分类计数原理,也叫做加法原理.完成一件事,需要分成几个步骤,每一步的完成有多种不同的方法,则完成这件事的不同方法种数是各种不同的方法数的乘积,这就是分步计数原理,也叫做乘法原理.
小王同学参加某高中学校进行的自主招生考试,本次考试共有1000人参加.
(1)1000人参加自招考试,有300人可以享受加分政策,且有10,20,30,60四个档次,小王想获得至少30分的加分,那么概率为多少?
(2)若该高中的中考录取分数线为530分,小王估得中考分数可能在500-509,510-519,520-529三个分段,
①若小王的中考分数在510~519分段,则小王被该高中录取的概率为多少?
②若小王的中考分数在三个分数段对应的概率分别为![]() ,
,![]() ,
,![]() ,则小王被该高中录取的概率为多少?
,则小王被该高中录取的概率为多少?
加分 | 人数 |
10 | 30 |
20 | 90 |
30 | 150 |
60 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
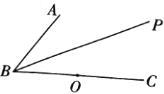
【题目】如图所示,在平面内,给定不在同一直线上的点![]() ,
,![]() ,
,![]() ,射线
,射线![]() 是
是![]() 的平分线,点
的平分线,点![]() 到点
到点![]() ,
,![]() ,
,![]() 的距离均等于
的距离均等于![]() (
(![]() 为常数),到点
为常数),到点![]() 的距离等于
的距离等于![]() 的所有点组成图形
的所有点组成图形![]() ,图形
,图形![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)过点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,作
,作![]() 于点
于点![]() ,延长
,延长![]() 交图形
交图形![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,求直线
,求直线![]() 与图形
与图形![]() 的公共点个数.
的公共点个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组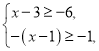
![]() 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_______________;
(Ⅱ)解不等式②,得_______________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
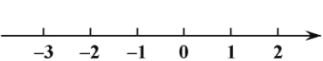
(Ⅳ)原不等式组的解集为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com