
分析 在y轴上找一点P,使△APB为等腰三角形,则需要分类讨论:以AB为腰和以AB为底两种情况进行解答.
解答 解:∵A(3,0),B(0,2),
∴AB=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
①以AB为底时,
作出线段AB的垂直平分线和y轴交于P点,
∴点P的坐标为(0,-$\frac{5}{4}$).
②以AB为腰时,符合条件的点P的坐标是:(0,2$+\sqrt{13}$),(0,-2),(0,2-$\sqrt{13}$),
综上所述,满足条件的P的坐标是:(0,-$\frac{5}{4}$)、(0,2+$\sqrt{13}$)、(0,-2)、(0,2-$\sqrt{13}$),
故答案为:(0,-$\frac{5}{4}$)、(0,2+$\sqrt{13}$)、(0,-2)、(0,2-$\sqrt{13}$),
点评 本题考查了等腰三角形的判定及坐标与图形的性质以及垂直平分线的性质,同时考查了学生动手作图的能力.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 3cm,5cm,10cm | B. | 5cm,4cm,9cm | C. | 4cm,6cm,9cm | D. | 5cm,7cm,13cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
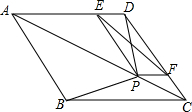 如图,在菱形ABCD中,P是对角线AC上任一点(不与A,C重合),连接BP,DP,过P作PE∥CD交AD于E,过P作PF∥AD交CD于F,连接EF.
如图,在菱形ABCD中,P是对角线AC上任一点(不与A,C重合),连接BP,DP,过P作PE∥CD交AD于E,过P作PF∥AD交CD于F,连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | $\frac{1}{4}$ | $\frac{1}{2}$ | 1 | 2 | 4 | 8 |
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 图1是一张Rt△ABC纸片,如果用两张相同的这种纸片恰好能拼成一个正三角形(图2),那么在Rt△ABC中,sinB的值是$\frac{\sqrt{3}}{2}$.
图1是一张Rt△ABC纸片,如果用两张相同的这种纸片恰好能拼成一个正三角形(图2),那么在Rt△ABC中,sinB的值是$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
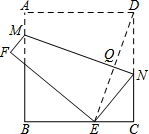 如图,正方形纸片ABCD的边长为4cm,点M、N分别在边AB、CD上.将该纸片沿MN折叠,使点D落在边BC上,落点为E,MN与DE相交于点Q.随着点M的移动,点Q移动路线长度的最大值是( )
如图,正方形纸片ABCD的边长为4cm,点M、N分别在边AB、CD上.将该纸片沿MN折叠,使点D落在边BC上,落点为E,MN与DE相交于点Q.随着点M的移动,点Q移动路线长度的最大值是( )| A. | 4cm | B. | 2cm | C. | $\sqrt{2}$cm | D. | 1cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com