
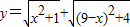 ,当x为何值时,y的值最小,并求出这个最小值.
,当x为何值时,y的值最小,并求出这个最小值.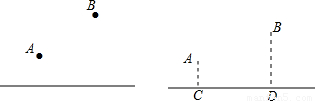
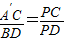 ,所以
,所以 ,求解即可;
,求解即可;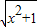 ,PB=
,PB=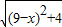 ,由(2)知,当A´,P,B共线时,PA´+PB=y最小,
,由(2)知,当A´,P,B共线时,PA´+PB=y最小,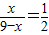 ,求解即可.
,求解即可.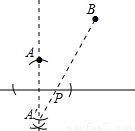 (2分)
(2分)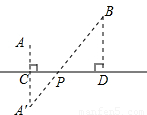
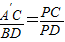 ,(4分)
,(4分)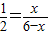 ,解得x=2,
,解得x=2,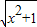 ,PB=
,PB=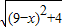 ,(7分)
,(7分)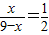 ,解得x=3,
,解得x=3,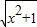 +
+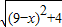 值最小,(9分)
值最小,(9分)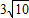 .(10分)
.(10分)

科目:初中数学 来源: 题型:阅读理解
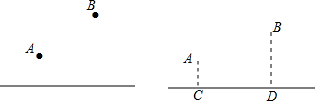 面问题:若y=
面问题:若y=| x2+1 |
| (9-x)2+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 面问题:若
面问题:若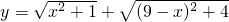 ,当x为何值时,y的值最小,并求出这个最小值.
,当x为何值时,y的值最小,并求出这个最小值.查看答案和解析>>
科目:初中数学 来源:四川省中考真题 题型:解答题
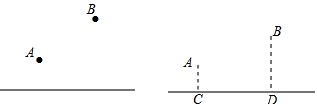
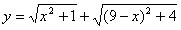 ,当x为何值时,y的值最小,并求出这个最小值。
,当x为何值时,y的值最小,并求出这个最小值。查看答案和解析>>
科目:初中数学 来源:2006年四川省内江市中考数学试卷(课标卷)(解析版) 题型:解答题
 ,当x为何值时,y的值最小,并求出这个最小值.
,当x为何值时,y的值最小,并求出这个最小值.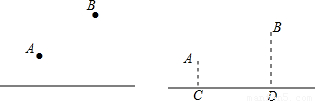
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com