
【题目】已知抛物线![]() (a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.
(a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.
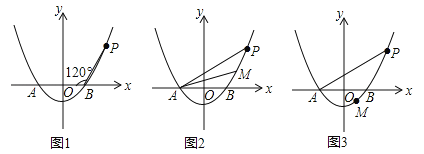
(1)求抛物线的解析式.
(2)设点M(m,n)为抛物线上的一个动点,且在曲线PA上移动.
①当点M在曲线PB之间(含端点)移动时,是否存在点M使△APM的面积为![]() ?若存在,求点M的坐标;若不存在,请说明理由.
?若存在,求点M的坐标;若不存在,请说明理由.
②当点M在曲线BA之间(含端点)移动时,求|m|+|n|的最大值及取得最大值时点M的坐标.
【答案】(1)![]() ;(2)①存在,M(3,
;(2)①存在,M(3,![]() );②M(
);②M(![]() ,
,![]() )或(
)或(![]() ,
,![]() )时,|m|+|n|的最大值为
)时,|m|+|n|的最大值为![]() .
.
【解析】
试题分析:(1)先求出A、B两点坐标,然后过点P作PC⊥x轴于点C,根据∠PBA=120°,PB=AB,分别求出BC和PC的长度即可得出点P的坐标,最后将点P的坐标代入二次函数解析式即;
(2)①过点M作ME⊥x轴于点E,交AP于点D,分别用含m的式子表示点D、M的坐标,然后代入△APM的面积公式![]() DMAC,根据题意列出方程求出m的值;
DMAC,根据题意列出方程求出m的值;
②根据题意可知:n<0,然后对m的值进行分类讨论,当﹣2≤m≤0时,|m|=﹣m;当0<m≤2时,|m|=m,列出函数关系式即可求得|m|+|n|的最大值.
试题解析:(1)如图1,令y=0代入![]() ,∴
,∴![]() ,∵a>0,∴
,∵a>0,∴![]() ,∴x=±2,∴A(﹣2,0),B(2,0),∴AB=4,过点P作PC⊥x轴于点C,∴∠PBC=180°﹣∠PBA=60°,∵PB=AB=4,∴cos∠PBC=
,∴x=±2,∴A(﹣2,0),B(2,0),∴AB=4,过点P作PC⊥x轴于点C,∴∠PBC=180°﹣∠PBA=60°,∵PB=AB=4,∴cos∠PBC=![]() ,∴BC=2,由勾股定理可求得:PC=
,∴BC=2,由勾股定理可求得:PC=![]() ,∵OC=OC+BC=4,∴P(4,
,∵OC=OC+BC=4,∴P(4,![]() ),把P(4,
),把P(4,![]() )代入
)代入![]() ,∴
,∴![]() =16a﹣4a,∴a=
=16a﹣4a,∴a=![]() ,∴抛物线解析式为:
,∴抛物线解析式为:![]() ;
;
(2)∵点M在抛物线上,∴![]() ,∴M的坐标为(m,
,∴M的坐标为(m,![]() );
);
①当点M在曲线PB之间(含端点)移动时,∴2≤m≤4,如图2,过点M作ME⊥x轴于点E,交AP于点D,设直线AP的解析式为y=kx+b,把A(﹣2,0)与P(4,![]() )代入y=kx+b,得:
)代入y=kx+b,得: ,解得:
,解得: ,∴直线AP的解析式为:
,∴直线AP的解析式为:![]() ,令x=m代入
,令x=m代入![]() ,∴
,∴![]() ,∴D的坐标为(m,
,∴D的坐标为(m,![]() ),∴DM=
),∴DM=![]() =
=![]() ,∴S△APM=
,∴S△APM=![]() DMAE+
DMAE+![]() DMCE
DMCE
=![]() DM(AE+CE)=
DM(AE+CE)=![]() DMAC=
DMAC=![]() ,当S△APM=
,当S△APM=![]() 时,∴
时,∴![]() =
=![]() ,∴解得m=3或m=﹣1,∵2≤m≤4,∴m=3,此时,M的坐标为(3,
,∴解得m=3或m=﹣1,∵2≤m≤4,∴m=3,此时,M的坐标为(3,![]() );
);
②当点M在曲线BA之间(含端点)移动时,∴﹣2≤m≤2,n<0,当﹣2≤m≤0时,∴|m|+|n|=﹣m﹣n=![]() =
=![]() ,当m=
,当m=![]() 时,∴|m|+|n|可取得最大值,最大值为
时,∴|m|+|n|可取得最大值,最大值为![]() ,此时,M的坐标为(
,此时,M的坐标为(![]() ,
,![]() ),当0<m≤2时,∴|m|+|n|=m﹣n=
),当0<m≤2时,∴|m|+|n|=m﹣n=![]() =
=![]() ,当m=
,当m=![]() 时,∴|m|+|n|可取得最大值,最大值为
时,∴|m|+|n|可取得最大值,最大值为![]() ,此时,M的坐标为(
,此时,M的坐标为(![]() ,
,![]() ),综上所述,当点M在曲线BA之间(含端点)移动时,M的坐标为(
),综上所述,当点M在曲线BA之间(含端点)移动时,M的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )时,|m|+|n|的最大值为
)时,|m|+|n|的最大值为![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;

2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】调查某班级的学生对数学老师的喜欢程度,下列最具有代表性的样本是( )
A. 调查单数学号的学生 B. 调查所有的班级干部
C. 调查全体女生 D. 调查数学兴趣小组的学生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京津城际铁路开通运营,预计高速列车在北京、天津间单程直达运行时间为半小时.某次试运行时,试验列车由北京到天津的行驶时间比预计时间多用了6分钟,由天津返回北京行驶时间与预计时间相同.如果这次试车时,由天津返回北京比去天津时平均每小时多行驶了40千米,那么这次试车时由北京到天津的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视机厂生产甲、乙、丙三种不同型号的电视机,出厂价分别为1200元,2000元,2200元.某商场同时从该厂购进其中两种不同型号的电视机共50台,正好用去80000元.
(1)该商场有几种进货方案?(写出演算步骤)
(2)若该商场销售甲、乙、丙种电视机每台可分别获利200元,250元,300元,如何进货可使销售时获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设京西绿色走廊,改善永定河水质,某治污公司决定购买10台污水处理设备.现有A、B两种型号的设备,其中每台的价格与月处理污水量如下表:

经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求x、y的值;
(2)如果治污公司购买污水处理设备的资金不超过105万元,求该治污公司有哪几种购买方案;
(3)在(2)的条件下,如果月处理污水量不低于2040吨,为了节约资金,请为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种商品,甲的进货单价比乙的进货单价高20元,已知20个甲商品的进货总价与25个乙商品的进货总价相同.
(1)求甲、乙商品的进货单价;
(2)若甲、乙两种商品共进货100件,要求两种商品的进货总价不高于9000元,同时甲商品按进价提高10%后的价格销售,乙商品按进价提高25%后的价格销售,两种商品全部售完后的销售总额不低于10480元,问有哪几种进货方案?
(3)在条件(2)下,并且不再考虑其他因素,若甲、乙两种商品全部售完,哪种方案利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
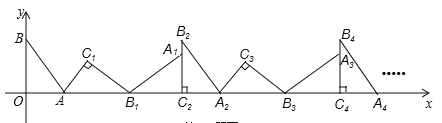
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则点B2016的坐标为______________.
,0),B(0,2),则点B2016的坐标为______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com