
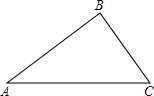
 如图:在△ABC中,∠C=45°,BC=2$\sqrt{2}$,AC=6,求tanA和△ABC的面积.
如图:在△ABC中,∠C=45°,BC=2$\sqrt{2}$,AC=6,求tanA和△ABC的面积. 分析 作BD⊥AC,根据∠C=45°,BC=2$\sqrt{2}$,AC=6,可得BD,CD的长,从而可以求得AD的长,从而可以解答本题.
解答 解:作BD⊥AC于点D,如下图所示:
∵∠C=45°,BC=2$\sqrt{2}$,BD⊥AC,
∴∠BDC=90°,BD=CD,BD2+CD2=BC2.
∴BD=CD=2.
∵AC=6,CD=2,
∴AD=4.
∴tanA=$\frac{BD}{AD}=\frac{2}{4}=\frac{1}{2}$,${S}_{△ABC}=\frac{AC×BD}{2}=\frac{6×2}{2}=6$.
即tanA=$\frac{1}{2}$,△ABC的面积是6.
点评 本题考查解直角三角形、三角形的面积,解题的关键是作合适的辅助线,明确三角函数指的是哪两条边的比值.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,小红将两个直角三角形AOB,COD摆放在桌面上,使得它们的直角顶点重合在一起,小红得到出两个结论:(1)∠AOC=∠BOD;(2)∠AOD与∠BOC互补,请你判断她得出的两个结论是否正确,并说明理由.
如图所示,小红将两个直角三角形AOB,COD摆放在桌面上,使得它们的直角顶点重合在一起,小红得到出两个结论:(1)∠AOC=∠BOD;(2)∠AOD与∠BOC互补,请你判断她得出的两个结论是否正确,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com