
【题目】ΔABC、ΔCDE都是等边三角形,AD、BE相交于点O,点M、点N分别是线段AD、BE的中点.
(1)证明: AD=BE.(2)求∠DOE的角度。(3)证明:ΔMNC是等边三角形.

【答案】(1)详见解析;(2)60°;(3)详见解析
【解析】
提示:先证明ΔACD≌BCE(SAS).利用第(1)问证明的结论,用三角形内角和求出∠DOE=60°,易得ΔACM≌ΔBCN(SAS),从而得到ΔCMN为等边三角形.
证明:(1)∵△ABC、△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∵∠ACB+∠BCD=∠ACD,
∠DCE+∠BCD=∠BCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
AC=BC
∠ACD=∠BCE
CD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE;
(2)由(1)知∵△ACD≌△BCE,
∴∠ACD=∠BEC,
∵三角形DCE是等边三角形,
∴∠CED=∠CDE=60°
∴∠ADE+∠BED=∠ADC+∠CDE+∠BED=∠ADC+60°+∠BED=∠CED+60°=60°+60°=120°
∴∠DOE=180°-(∠ADE+∠BED)=60°
(3)∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∵点M、N分别是线段AD、BE的中点,AD=BE,
∴AM=BN,
在△ACM和△BCN中,
AC=BC
∠CAD=∠CBE
AM=BN,
∴△ACM≌△BCN(SAS),
∴CM=CN,∠ACM=∠BCN,
∴∠MCN=∠BCM+∠BCN=∠BCM+∠ACM=∠ACB=60°,
∴△MNC是等边三角形.


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1、S2、S3、S4.则S1﹣S2+S3+S4等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解余姚市对“垃圾分类知识”的知晓程度,某数学学习兴趣小组对市民进行随机抽样的问卷调查,调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”、“D.不太了解”四个等级进行统计,并将统计结果绘制成了如下两幅不完整的统计图(图1、图2),请根据图中的信息解答下列问题.
(1)这次调查的市民人数为 人,图2中,m=
(2)补全图1中的条形统计图;
(3)据统计,2017年余姚约有市民140万人,那么根据抽样调查的结果,可估计对“垃圾分类知识”的知晓程度为“B.了解”的市民约有多少万人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在长方形![]() 中,AB=4cm,BC=6cm,点
中,AB=4cm,BC=6cm,点![]() 为
为![]() 中点,如果点
中点,如果点![]() 在线段
在线段![]() 上以每秒2cm的速度由点
上以每秒2cm的速度由点![]() 向点
向点![]() 运动,同时,点
运动,同时,点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 运动.设点
运动.设点![]() 运动时间为
运动时间为![]() 秒,若某一时刻△BPE与△CQP全等,求此时
秒,若某一时刻△BPE与△CQP全等,求此时![]() 的值及点
的值及点![]() 的运动速度.
的运动速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
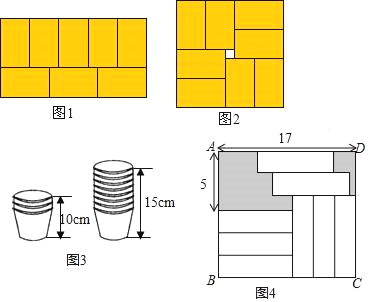
小明是个爱动脑筋的学生,他在学习了二元一次方程组后遇到了这样一道题目:现有8个大小相同的长方形,可拼成如图1、2所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,求每个小长方形的面积.
小明设小长方形的长为x,宽为y,观察图形得出关于x、y的二元一次方程组,解出x、y的值,再根据长方形的面积公式得出每个小长方形的面积.
解决问题:
(1)请按照小明的思路完成上述问题:求每个小长方形的面积;
(2)某周末上午,小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图3所示.若小明把13个纸杯整齐叠放在一起时,它的高度约是 cm;
(3)小明进行自主拓展学习时遇到了以下这道题目:如图,长方形ABCD中放置8个形状、大小都相同的小长方形(尺寸如图4),求图中阴影部分的面积,请给出解答过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com