
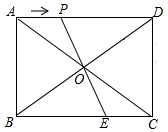
 如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O,点P从点A出发,沿AD方向匀速运动,速度为2cm/s,当OD平分∠COP时,运动时间为$\frac{56}{39}$s.
如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O,点P从点A出发,沿AD方向匀速运动,速度为2cm/s,当OD平分∠COP时,运动时间为$\frac{56}{39}$s. 分析 如图,作OG⊥BD交AD于G,作OH⊥AD于H,GM⊥AC于M,GN⊥OP于N.由△DOG∽△DAB可得DG=$\frac{25}{4}$,AG=$\frac{7}{4}$,由$\frac{{S}_{△AOG}}{{S}_{△GOP}}$=$\frac{AG}{PG}$=$\frac{\frac{1}{2}•OA•GM}{\frac{1}{2}•OP•GN}$=$\frac{OA}{OP}$,设PG=x,OP=y,可得$\frac{\frac{7}{4}}{x}$=$\frac{5}{y}$,推出y=$\frac{20}{7}$x,在Rt△OPH中,OP=y,OH=3,PH=$\frac{9}{4}-x$,可得y2=($\frac{9}{4}$-x)2+32,解方程组即可解决问题.
解答 解:如图,作OG⊥BD交AD于G,作OH⊥AD于H,GM⊥AC于M,GN⊥OP于N.
∵四边形ABCD是矩形,
∴AB=CD=6,BC=AD=8,
易知AC=BD=10,OA=OB=OC=OD=5,
由△DOG∽△DAB可得DG=$\frac{25}{4}$,AG=$\frac{7}{4}$,
∵∠DOP=∠DOC=∠AOB,∠GOD=∠GOB=90°,
∴∠AOG=∠GOP,
∴GM=GN,
∴$\frac{{S}_{△AOG}}{{S}_{△GOP}}$=$\frac{AG}{PG}$=$\frac{\frac{1}{2}•OA•GM}{\frac{1}{2}•OP•GN}$=$\frac{OA}{OP}$,设PG=x,OP=y,
∴$\frac{\frac{7}{4}}{x}$=$\frac{5}{y}$,
∴y=$\frac{20}{7}$x,
在Rt△OPH中,OP=y,OH=3,PH=$\frac{9}{4}-x$,
∴y2=($\frac{9}{4}$-x)2+32,
∴($\frac{20}{7}$x)2=($\frac{9}{4}$-x)2+32,
解得x=$\frac{175}{156}$(负根已经舍弃),
∴AP=AG+GP=$\frac{7}{4}$+$\frac{175}{156}$=$\frac{112}{39}$,
∴t=$\frac{112}{39}$÷2=$\frac{56}{39}$.
故答案为$\frac{56}{39}$.
点评 本题考查矩形的性质、角平分线的性质定理、勾股定理、相似三角形的性质、二元二次方程组等知识,解题的关键是学会添加常用辅助线,学会利用参数构建方程组解决问题,属于中考填空题中的压轴题.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 50×10-7 | B. | 50×10-5 | C. | 50×10-3 | D. | 5×10-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
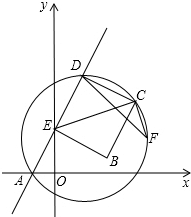 如图,直线y=2x+2与x轴,y轴分别交于A,E两点,D是第一象限内直线y=2x+2上运动的一个动点,以ED为边作正方形EDCB,连结CE,作EC⊥CF与过A,D,C三点的圆交于点F,连结DF.
如图,直线y=2x+2与x轴,y轴分别交于A,E两点,D是第一象限内直线y=2x+2上运动的一个动点,以ED为边作正方形EDCB,连结CE,作EC⊥CF与过A,D,C三点的圆交于点F,连结DF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 快、慢两车分别从相距480km的甲,乙两地同时出发,匀速行驶,相向而行,途中慢车因故停留了1小时,然后继续以原速驶向甲地,到达甲地后即停止行驶;快车到达乙地后,立即按原路原速返回甲地(调头时间忽略不计).如图是快、慢两车距乙地路程y(km)与所用时间x(h)之间的函数图象,则当两车第一次相遇时,快车距离甲地的路程是320千米.
快、慢两车分别从相距480km的甲,乙两地同时出发,匀速行驶,相向而行,途中慢车因故停留了1小时,然后继续以原速驶向甲地,到达甲地后即停止行驶;快车到达乙地后,立即按原路原速返回甲地(调头时间忽略不计).如图是快、慢两车距乙地路程y(km)与所用时间x(h)之间的函数图象,则当两车第一次相遇时,快车距离甲地的路程是320千米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com