
【题目】已知:如图,四边形ABCD是平行四边形,延长BA至点E,使AE=AB,连接CE、DE、AC,CE与AD交于点F.

(1)求证:四边形ACDE是平行四边形;
(2)若∠AFC=2∠B.求证:四边形ACDE是矩形.
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),矩形OABC的边OA、OC在坐标轴上,点B坐标为(5,4),点P是射线BA上的一动点,把矩形OABC沿着CP折叠,点B落在点D处.
(1)当点C、D、A共线时,AD= ;
(2)如图(2),当点P与点A重合时,CD与x轴交于点E,过点E作EF⊥AC,交BC于点F,请判断四边形AECF的形状,并说明理由;
(3)若点D正好落在x轴上,请直接写出点P的坐标: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足为Q,连接AP.

(1)试说明不论点P在BC边上何处时,都有△PBQ与△ABC相似;
(2)若Rt△AQP≌Rt△ACP≌Rt△BQP,求tanB的值;
(3)已知AC=3,BC=4,当BP为何值时,△AQP面积最大,并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(1)(-16![]() )-(-10
)-(-10![]() )-(1
)-(1![]() );(2)(-8)×(-4)-80÷(-6)
);(2)(-8)×(-4)-80÷(-6)
(3)—|![]() |—|-
|—|-![]() ×
×![]() |—|—3|;(4)18+32÷(-2)2—(—4)2×5
|—|—3|;(4)18+32÷(-2)2—(—4)2×5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 是
是![]() 边上一动点(不与点
边上一动点(不与点![]() 重合),延长
重合),延长![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)填空:
①当![]() 的值为_______时,四边形
的值为_______时,四边形![]() 是矩形;
是矩形;
②当![]() 的值为______时,四边形
的值为______时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让学生能更加了解温州历史,某校组织七年级师生共480人参观温州博物馆.学校向租车公司租赁A、B两种车型接送师生往返,若租用A型车3辆,B型车6辆,则空余15个座位;若租用A型车5辆,B型车4辆,则15人没座位.
(1)求A、B两种车型各有多少个座位;
(2)若A型车日租金为350元,B型车日租金为400元,且租车公司最多能提供7辆B型车,应怎样租车能使座位恰好坐满且租金最少,并求出最少租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点都在方格线的交点(格点)上.
(1)将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′,请在图中画出△A′B′C′.
(2)将△ABC向上平移1个单位,再向右平移5个单位得到△A″B″C″,请在图中画出△A″B″C″.
(3)若将△ABC绕原点O旋转180°,A的对应点A1的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
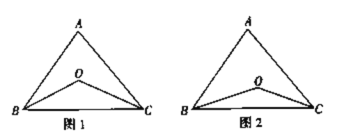
【题目】已知任意一个三角形的三个内角的和是180°,如图1,在ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O.
(1)若∠A=70°,求∠BOC的度数;
(2)若∠A=α,求∠BOC的度数;
(3)如图2,若BO、CO分别是∠ABC、∠ACB的三等分线,也就是∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A=α,求∠BOC的度数.
∠ACB,∠A=α,求∠BOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com