
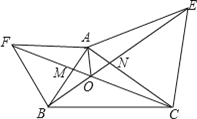
【题目】如图,已知AF=AB,∠FAB=60°,AE=AC,∠EAC=60°,CF和BE交于O点,则下列结论:①CF=BE;②∠COB=120°;③OA平分∠FOE;④OF=OA+OB.其中正确的有_____.
【答案】①②③④.
【解析】
结合等边三角形△ABF和△ACE的性质,利用SAS可证△ABE≌△AFC,由全等三角形的性质可知①正确;由三角形内角和为180度易求∠BOC的度数,可知②正确;连接AO,过A分别作AP⊥CF与P,AM⊥BE于Q,由S△ABE=S△AFC可知AP=AQ,利用HL定理可证![]() ,易知OA平分∠FOE,所以③正确;在OF上截取OD=OB,利用SAS可证△FBD≌△ABO,由全等三角形对应边相等易得OF= OA+OB,故④正确.
,易知OA平分∠FOE,所以③正确;在OF上截取OD=OB,利用SAS可证△FBD≌△ABO,由全等三角形对应边相等易得OF= OA+OB,故④正确.
解:∵△ABF和△ACE是等边三角形,
∴AB=AF,AC=AE,∠FAB=∠EAC=60°,
∴∠FAB+∠BAC=∠EAC+∠BAC,即∠FAC=∠BAE,
在△ABE与△AFC中,
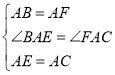 ,
,
∴△ABE≌△AFC(SAS),
∴BE=FC,∠AEB=∠ACF,故①正确;
∵∠EAN+∠ANE+∠AEB=180°,∠CON+∠CNO+∠ACF=180°,∠ANE=∠CNO,∴∠CON=∠CAE=60°=∠MOB,
∴∠BOC=180°﹣∠CON=120°,故②正确;
连接AO,过A分别作AP⊥CF与P,AM⊥BE于Q,如图1,
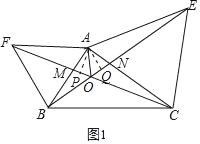
∵△ABE≌△AFC,∴S△ABE=S△AFC,∴![]() CFAP=
CFAP=![]() BEAQ,∵CF=BE,∴AP=AQ,
BEAQ,∵CF=BE,∴AP=AQ,
![]() ,∴OA平分∠FOE,所以③正确;
,∴OA平分∠FOE,所以③正确;
如图2,在OF上截取OD=OB,
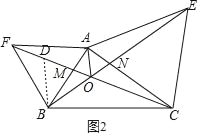
∵∠BOF=60°,∴△OBD是等边三角形,∴BD=BO,∠DBO=60°,∴∠FBD=∠ABO.
∵BF=AB,∴△FBD≌△ABO(SAS),∴DF=OA,∴OF=DF+OD=OA+OB,故④正确.
故答案为:①②③④.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE是两个不全等的等腰直角三角形,其中点B与点D是直角顶点,现固定△ABC,而将△ADE绕点A在平面内旋转.
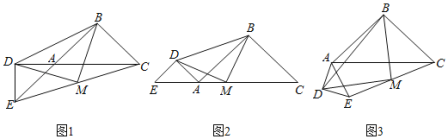
(1)如图1,当点D在CA延长线上时,点M为EC的中点,求证:△DMB是等腰三角形.
(2)如图2,当点E在CA延长线上时,M是EC上一点,若△DMB是等腰直角三角形,∠DMB为直角,求证:点M是EC的中点.
(3)如图3,当△ADE绕点A旋转任意角度时,线段EC上是否都存在点M,使△BMD为等腰直角三角形,若不存在,请举出反例;若存在,请予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F运算”:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的最小正整数),并且运算重复进行.例如:取n=26,则运算过程如图:
为奇数的最小正整数),并且运算重复进行.例如:取n=26,则运算过程如图:
![]()
那么当n=9时,第2019次“F运算”的结果是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】机械表是日常生活中常见的一类钟表,与电子表不同,机械表受环境、机芯等因素的影响常会产生走时误差.现为了比较市场上甲、乙两款机械表的精准度,从两款表中,各随机抽取一块进行每日走时误差的检测,连续检测10天,两款表每日走时误差的统计数据如图(单位:秒):
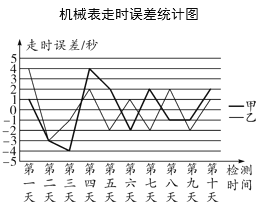
(1)甲、乙两种机械表的平均走时误差分别是多少?
(2)小明现计划购买一块机械表,如果仅从走时的准确度考虑,你会推荐他购买甲、乙哪一种,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2, 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
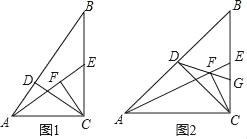
【题目】已知:如图1,△ABC中,∠ACB=90°,CD⊥AB于D,E为BC中点,CF⊥AE于F.
(1)求证:4CE2=BDAB;
(2)若2∠DCF=∠ECF,求cos∠ECF的值;
(3)如图2,DF延长线交BC于G,若AC=BC,EG=1,则DG= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 和反比例函数
和反比例函数![]() 的图象都经过点
的图象都经过点![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图象上,连接
的图象上,连接![]() .
.
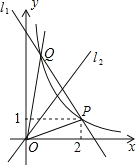
(1)求直线![]() 和反比例函数的解析式;
和反比例函数的解析式;
(2)直线![]() 经过点
经过点![]() 吗?请说明理由;
吗?请说明理由;
(3)当直线![]() 与反比例数
与反比例数![]() 图象的交点在
图象的交点在![]() 两点之间.且将
两点之间.且将![]() 分成的两个三角形面积之比为
分成的两个三角形面积之比为![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
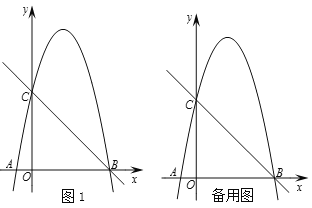
(1)求抛物线的函数表达式;
(2)若点P是位于直线BC上方抛物线上的一个动点,求△BPC面积的最大值;
(3)若点D是y轴上的一点,且以B,C,D为顶点的三角形与![]() 相似,求点D的坐标;
相似,求点D的坐标;
(4)若点E为抛物线的顶点,点F(3,a)是该抛物线上的一点,在![]() 轴、
轴、![]() 轴上分别找点M、N,使四边形EFMN的周长最小,求出点M、N的坐标.
轴上分别找点M、N,使四边形EFMN的周长最小,求出点M、N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,延长BC到点D,点O是AC边上的一个动点,过点O作直线MN∥BC,MN分别交∠ACB、∠ACD的平分线于E,F两点,连接AE、AF,在下列结论中:①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形,其中正确的有( )

A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com