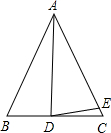练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．如图，在△ABC中，AB=AC，AD=AE，∠BAD=30°，∠EDC的度数是（　　）
    A．10°B．15°C．20°D．25°

    分析 可以设∠EDC=x，∠B=∠C=y，根据∠ADE=∠AED=x+y，∠ADC=∠B+∠BAD即可列出方程，从而求解．

    解答 解：设∠EDC=x，∠B=∠C=y，
    ∠AED=∠EDC+∠C=x+y，
    又因为AD=AE，所以∠ADE=∠AED=x+y，
    则∠ADC=∠ADE+∠EDC=2x+y，
    又因为∠ADC=∠B+∠BAD，
    所以 2x+y=y+30，
    解得x=15，
    所以∠EDC的度数是15°．
    故选B．

    点评 本题主要考查了等腰三角形的性质，等边对等角．正确确定相等关系列出方程是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．如图1，已知射线CB∥OA，∠C=∠OAB=120°，E1，F在CB上，且满足∠FOB=∠FBO，OE1平分∠COF．
    （1）求∠E1OB的度数；
    （2）若向右平行移动AB，其它条件不变，那么∠OBC：∠OFC的值是否发生变化？若变化，找出其中规律，若不变，求出这个比值；
    （3）如图2，若OE2平分∠COE1交CB于E2，OE3平分∠COE2交CB于E3，…，以此类推直到OEn平分∠COEn-1．若∠BOA=x，当n=4时，求∠OE4C．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．如图，已知在正方形网格中的两个格点三角形是位似形，它们的位似中心是（　　）
    A．点AB．点BC．点CD．点D

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．如图，AB=AC，D、E在BC上且AD=AE，AF⊥BC于点F则图中全等三角形有（　　）
    A．1对B．2对C．3对D．4对

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

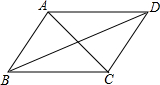    14．如图，下列条件不能够判定AB∥DC的是（　　）
    A．∠BAC=∠ACDB．∠DCB+∠ABC=180°C．∠ABD=∠BDCD．∠DAC=∠BCA

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．如图，矩形ABCD中，AB=8，BC=6，点E在边AB上，点F在边CD上，点G、H在对角线AC上，若四边形EGFH是菱形，则AE的长是（　　）
    A．6B．6.25C．6.5D．7

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

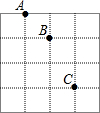    11．如图，利用平面直角坐标系画出的正方形网格中，若A（0，2），B（1，1），则点C的坐标为（　　）
    A．（1，-2）B．（2，1）C．（1，-1）D．（2，-1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．甲和乙一起做游戏，下列游戏规则对双方公平的是（　　）
    A．在一个装有2个红球和3个白球（每个球除颜色外都相同）的袋中任意摸出一球，摸到红球甲获胜，摸到白球乙获胜；
    B．从标有号数1到100的100张卡片中，随意抽取一张，抽到号数为奇数甲获胜，否则乙获胜；
    C．任意掷一枚质地均匀的骰子，掷出的点数小于4则甲获胜，掷出的点数大于4则乙获胜；
    D．让小球在如图所示的地板上自由地滚动，并随机地停在某块方块上，若小球停在黑色区域则甲获胜，若停在白色区域则乙获胜

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．先化简，再求值$\frac{x-4}{x-1}$÷（x+1-$\frac{15}{x-1}$）的值，其中x=8sin30°+2cos45°．

    查看答案和解析>>

    同步练习册答案