
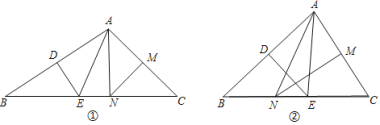
【题目】在![]() 中,
中,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() 、
、![]() .
.
⑴如图①,若![]() ,求
,求![]() 的度数;
的度数;
⑵如图②,若![]() ,求
,求![]() 的度数;
的度数;
⑶若![]()
![]() ,直接写出用
,直接写出用![]() 表示
表示![]() 大小的代数式.
大小的代数式.
【答案】(1)∠EAN=44°;(2)∠EAN=16°;(3)当0<α<90°时,∠EAN=180°-2α;当α>90°时,∠EAN=2α-180°.
【解析】
(1)根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,再根据等边对等角可得∠BAE=∠B,同理可得,∠CAN=∠C,然后利用三角形的内角和定理求出∠B+∠C,再根据∠EAN=∠BAC-(∠BAE+∠CAN)代入数据进行计算即可得解;
(2)同(1)的思路,最后根据∠EAN=∠BAE+∠CAN-∠BAC代入数据进行计算即可得解;
(3)根据前两问的求解,分α<90°与α>90°两种情况解答.
(1)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAC-∠BAE-∠CAN=∠BAC-(∠B+∠C),
在△ABC中,∠B+∠C=180°-∠BAC=180°-112°=68°,
∴∠EAN=∠BAC-(∠BAE+∠CAN)=112°-68°=44°;
(2)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN-∠BAC=(∠B+∠C)-∠BAC,
在△ABC中,∠B+∠C=180°-∠BAC=180°-82°=98°,
∴∠EAN=∠BAE+∠CAN-∠BAC=98°-82°=16°;
(3)当0<α<90°时,
∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN-∠BAC=(∠B+∠C)-∠BAC,
在△ABC中,∠B+∠C=180°-∠BAC=180°-α,
∴∠EAN=∠BAE+∠CAN-∠BAC=180°-α-α=180°-2α;
当α>90°时,
∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAC-∠BAE-∠CAN=∠BAC-(∠B+∠C),
在△ABC中,∠B+∠C=180°-∠BAC=180°-α,
∴∠EAN=∠BAC-(∠BAE+∠CAN)=α-(180°-α)=2α-180°.


科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其中的“面积法”给了李明灵感,他惊喜地发现;当两个全等的直角三角形如图(1)摆放时可以利用面积法”来证明勾股定理,过程如下
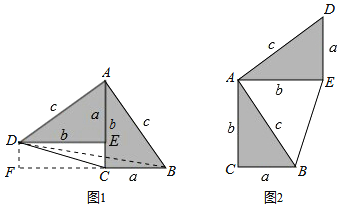
如图(1)∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作DF⊥BC交BC的延长线于点F,则DF=b-a
S四边形ADCB=![]()
S四边形ADCB=![]()
∴![]() 化简得:a2+b2=c2
化简得:a2+b2=c2
请参照上述证法,利用“面积法”完成如图(2)的勾股定理的证明,如图(2)中∠DAB=90°,求证:a2+b2=c2
查看答案和解析>>
科目:初中数学 来源: 题型:
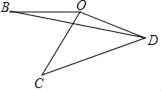
【题目】将线段OB绕点O逆时针旋转60°得到线段OC,继续旋转α(0°<α<120°)得到线段OD,连接CD.
(1)如图,连接BD,则∠BDC的大小=_____(度);
(2)将线段OB放在平面直角坐标系中,O是坐标原点,点B的坐标为(﹣6,0),以OB为斜边作Rt△OBE,使∠OBE=∠OCD,且点E在第三象限,若∠CED=90°,则α的大小=_____(度),点D的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
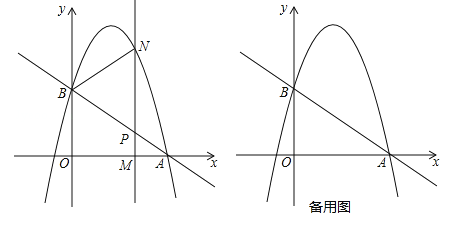
【题目】如图,抛物线y=﹣![]() +bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
+bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
(1)求直线AB的解析式和抛物线的解析式;
(2)如果点P是MN的中点,那么求此时点N的坐标;
(3)在对称轴的左侧是否存在点M使四边形OMPB的面积最大,如果存在求点M的坐标;不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学课外活动小组在学习了锐角三角函数后,组织了一次利用自制的测角仪测量古塔高度的活动.具体方法如下:在古塔前的平地上选择一点E,某同学站在E点用测角仪测得古塔顶的仰角为30°,从E向着古塔前进12米后到达点F,又测得古塔顶的仰角为45°,并绘制了如图的示意图(图中线段AE=BF=1.6米,表示测角的学生眼睛到地面的高度).请你帮着计算古塔CD的高度(结果保留整数,参考数据:![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°.
(1)如图1,点E在BC上,则线段AE和BD有怎样的关系?请直接写出结论(不需证明);
(2)若将△DCE绕点C旋转一定的角度得图2,则(1)中的结论是否仍然成立?请说明理由;
(3)当△DCE旋转到使∠ADC=90°时,若AC=5,CD=3,求BE的长.
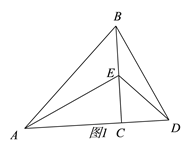
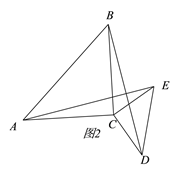
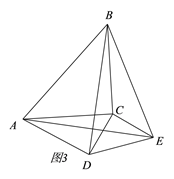
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人同时登山,甲乙两人距地面的高度![]() (米
(米![]() 与登山时间
与登山时间![]() (分
(分![]() 之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是 米![]() 分钟,乙在
分钟,乙在![]() 地提速时距地面的高度
地提速时距地面的高度![]() 为 米;
为 米;
(2)直接写出甲距地面高度![]() (米
(米![]() 和
和![]() (分
(分![]() 之间的函数关系式;
之间的函数关系式;
(3)若乙提速后,乙的速度是甲登山速度的3倍.请问登山多长时间时,乙追上了甲,此时乙距![]() 地的高度为多少米?
地的高度为多少米?
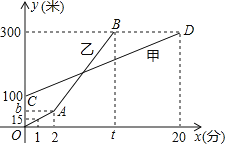
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com