
【题目】直线![]() 经过原点和点
经过原点和点![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求直线![]() 所对应的函数解析式;
所对应的函数解析式;
(2)当P在线段OA上时,设![]() 点横坐标为
点横坐标为![]() ,三角形
,三角形![]() 的面积为
的面积为![]() ,写出
,写出![]() 关于
关于![]() 的函数解析式,并指出自变量
的函数解析式,并指出自变量![]() 的取值范围;
的取值范围;
(3)当P在射线OA上时,在坐标轴上有一点![]() ,使
,使![]() (
(![]() 正整数),请直接写出点
正整数),请直接写出点![]() 的坐标(本小题只要写出结果,不需要写出解题过程)
的坐标(本小题只要写出结果,不需要写出解题过程)

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用待定系数法即可解决问题;
(2)利用三角形的面积公式计算即可;
(3)分两种情形分别求解即可.
(1)设直线l的解析式为y=kx,
把点A坐标代入得到6=3k,
∴k=2,
∴直线l的解析式为y=2x.
(2)∵P(x,2x),B(4,0),
∴S=![]() ×4×2x=4x,(0<x≤3);
×4×2x=4x,(0<x≤3);
(3)∵点B的坐标为(6,0),点C在坐标轴上,
①当点C在x轴上时,则△BOP和△COP是同高三角形,
∵S△BOP:S△COP=2:m,
∴![]() ,
,
∴OC=3m,
∴C(3m,0)或(-3m,0);
②当点C在x轴上时,则△BOP和△COP是同高三角形,
∵P(x,2x),S△BOP:S△COP=2:m,
∴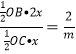 ,即
,即![]() ,
,
∴OC=6m,
∴C(0,6m)或(0,-6m).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
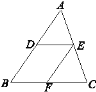
【题目】如图,点D,E分别在AB,AC上,DE∥BC,EF平分∠DEC,交BC于点F,且∠ABC=55°,∠C=70°.
(1)求∠DEF的度数;
(2)请判断EF与AB的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用![]() 表示不大于
表示不大于![]() 的最大整数,例如:
的最大整数,例如:![]() ,
,![]() ,
,![]() ;用
;用![]() 表示大于
表示大于![]() 的最小整数,例如:
的最小整数,例如:![]() ,
,![]() ,
,![]() .解决下列问题:
.解决下列问题:
(1)![]() = ,,
= ,,![]() = ;
= ;
(2)若![]() =2,则
=2,则![]() 的取值范围是 ;若
的取值范围是 ;若![]() =-1,则
=-1,则![]() 的取值范围是 ;
的取值范围是 ;
(3)已知![]() ,
,![]() 满足方程组
满足方程组![]() ,求
,求![]() ,
,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以O(0,0)、A(2,0)为顶点作正△OAP1 , 以点P1和线段P1A的中点B为顶点作正△P1BP2 , 再以点P2和线段P2B的中点C为顶点作△P2CP3 , …,如此继续下去,则第六个正三角形中,不在第五个正三角形上的顶点P6的坐标是 . 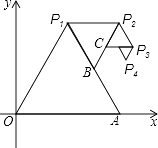
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题背景:已知,如图1,等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,AB=a,△ABC的面积为S,则有BC=![]() a,S=
a,S=![]() a2.
a2.
(2)迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
①求证:△ADB≌△AEC;
②求∠ADB的度数.
③若AD=2,BD=4,求△ABC的面积.
(3)拓展延伸:如图3,在等腰△ABC中,∠BAC=120°,在∠BAC内作射线AM,点D与点B关于射线AM轴对称,连接CD并延长交AM于点E,AF⊥CD于F,连接AD,BE.
①求∠EAF的度数;
②若CD=5,BD=2,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数1至2019按一定规律排列如下表:
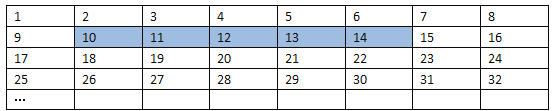
平移表中带阴影的方框,则方框中五个数的和可以是( )
A. 2010 B. 2018 C. 2019 D. 2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市举行的中学生安全知识竞赛中共有20道题.每一题答对得5分,答错或不答都扣3分.
(1)小李考了60分,那么小李答对了多少道题?
(2)小王获得二等奖(75~85分),请你算算小王答对了几道题?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店购进一批甲、乙两种款型时尚T恤衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)甲、乙两种款型的T恤衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完 这批T恤衫商店共获利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com