
分析 根据有理数的分类:有理数$\left\{\begin{array}{l}{整数\left\{\begin{array}{l}{正整数}\\{0}\\{负整数}\end{array}\right.}\\{分数\left\{\begin{array}{l}{正分数}\\{负分数}\end{array}\right.}\end{array}\right.$进行填空即可.
解答 解:非负整数集合:{ 10,0+66,2014},
整数集合:{-5,10,0+66,-16,2014}
负整数集合:{-5,-16}
正分数集合:{ 12$\frac{1}{3}$,0.01}
非正数集合:{-5,-7$\frac{2}{3}$,0,-2.15,-16}.
故答案为:{ 10,0+66,2014};{-5,10,0+66,-16,2014};{-5,-16};{ 12$\frac{1}{3}$,0.01};{-5,-7$\frac{2}{3}$,0,-2.15,-16}.
点评 此题主要考查了有理数分类,认真掌握正数、负数、整数、分数、正有理数、负有理数、非负数的定义与特点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
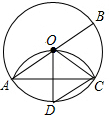 已知:如图,AB是⊙O的直径,AC是弦,将劣弧$\widehat{AC}$沿弦AC翻折与AB的交点恰好是圆心O,连接BC,作半径OD⊥AC.求证:四边形BCDO是菱形.
已知:如图,AB是⊙O的直径,AC是弦,将劣弧$\widehat{AC}$沿弦AC翻折与AB的交点恰好是圆心O,连接BC,作半径OD⊥AC.求证:四边形BCDO是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
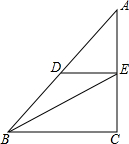 完成求解过程,并写出括号里的理由:
完成求解过程,并写出括号里的理由:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是等边三角形,D是BC上一点,∠ADE=60°,∠BCE=120°,CE、DE交于E;
如图,△ABC是等边三角形,D是BC上一点,∠ADE=60°,∠BCE=120°,CE、DE交于E;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com