
【题目】如图,菱形ABCD边长为6,∠BAD=120°,点E、F分别在AB、AD上且BE=AF,则EF的最小值为_____,

【答案】3![]()
【解析】
连接AC,根据菱形的性质得到∠B=60°,AB=BC,推出△ABC是等边三角形,得到AC=BC,∠B=∠CAF=60°,根据全等三角形的性质得到CE=CF,∠BCE=∠ACF,求得△CEF是等边三角形,得到EF=CE,于是得到当CE⊥AB时,CE最小,即EF最小,解直角三角形即可得到结论.
解:连接AC,
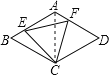
∵四边形ABCD是菱形,∠BAD=120°,
∴∠B=60°,AB=BC,
∴△ABC是等边三角形,
∴AC=BC,∠B=∠CAF=60°,
∵BE=AF,
∴△BCE≌△ACF(SAS),
∴CE=CF,∠BCE=∠ACF,
∴∠ECF=∠ACB=60°,
∴△CEF是等边三角形,
∴EF=CE,
∴当CE⊥AB时,CE最小,即EF最小,
∵CE⊥AB,
∴∠CEB=90°,
∵∠B=60°,
∴CE=![]() BC=3
BC=3![]() ,
,
∴EF的最小值为3![]() ,
,
故答案为:3![]() .
.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊缆A′B′=AB.AB垂直地面O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA=![]() ,sinA′=
,sinA′=![]() .
.
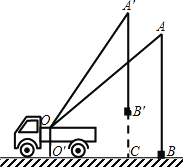
(1)求此重物在水平方向移动的距离BC;
(2)求此重物在竖直方向移动的距离B′C.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中(如图),已知二次函数
中(如图),已知二次函数![]() (其中a、b、c是常数,且a≠0)的图像经过点A(0,-3)、B(1,0)、C(3,0),联结AB、AC.
(其中a、b、c是常数,且a≠0)的图像经过点A(0,-3)、B(1,0)、C(3,0),联结AB、AC.
(1)求这个二次函数的解析式;
(2)点D是线段AC上的一点,联结BD,如果![]() ,求tan∠DBC的值;
,求tan∠DBC的值;
(3)如果点E在该二次函数图像的对称轴上,当AC平分∠BAE时,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小彬做了探究物体投影规律的实验,并提出了一些数学问题请你解答:
(1)如图1,白天在阳光下,小彬将木杆![]() 水平放置,此时木杆在水平地面上的影子为线段
水平放置,此时木杆在水平地面上的影子为线段![]() .
.
①若木杆![]() 的长为
的长为![]() ,则其影子
,则其影子![]() 的长为
的长为 ![]() ;
;
②在同一时刻同一地点,将另一根木杆![]() 直立于地面,请画出表示此时木杆
直立于地面,请画出表示此时木杆![]() 在地面上影子的线段
在地面上影子的线段![]() ;
;
(2)如图2,夜晚在路灯下,小彬将木杆![]() 水平放置,此时木杆在水平地面上的影子为线段
水平放置,此时木杆在水平地面上的影子为线段![]() .
.
①请在图中画出表示路灯灯泡位置的点![]() ;
;
②若木杆![]() 的长为
的长为![]() ,经测量木杆
,经测量木杆![]() 距离地面
距离地面![]() ,其影子
,其影子![]() 的长为
的长为![]() ,则路灯
,则路灯![]() 距离地面的高度为
距离地面的高度为![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
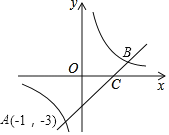
【题目】一次函数y1=x+m的图象与反比例函数y2=![]() 的图象相交于A(﹣1,﹣3)和点B,且与x轴交于点C.
的图象相交于A(﹣1,﹣3)和点B,且与x轴交于点C.
(1)求m及k的值.
(2)求点B、C坐标,并结合图形直接写出不等式0<x+m<![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
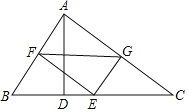
【题目】如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E是BC边上的一个动点(不与B,C重合),EF⊥AB,EG⊥AC,垂足分别为F,G.
(1)求证:![]() ;
;
(2)FD与DG是否垂直?若垂直,请给出证明;若不垂直,请说明理由;
(3)当![]() 的值为多少时,△FDG为等腰直角三角形?
的值为多少时,△FDG为等腰直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点D、E,F分别在△ABC的边AB、BC,AC上,联结DE、EF,且DE∥AC,那么下列说法错误的是( )
A.如果EF∥AB,那么AF:AC=BD:AB
B.如果AD:AB=CF:AC,那么EF∥AB
C.如果△EFC∽△ABC,那么 EF∥AB
D.如果EF∥AB,那么△EFC∽△BDE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,与x轴交于A、B(-1,0),与y轴交于C.下列结论错误的是( )
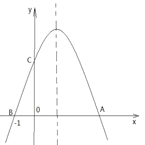
A.二次函数的最大值为a+b+cB.4a-2b+c﹤0
C.当y>0时,-1﹤x﹤3D.方程ax2+bx+c=-2解的情况可能是无实数解,或一个解,或二个解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com