
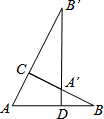
 如图,Rt△ABC中,∠ACB=90°,AC=1,BC=2.将△ABC绕顶点C旋转,点A转到BC边上的点A′处,点B转到点B′处.延长B′A′交AB于点D,则S△BA′D=$\frac{1}{5}$.
如图,Rt△ABC中,∠ACB=90°,AC=1,BC=2.将△ABC绕顶点C旋转,点A转到BC边上的点A′处,点B转到点B′处.延长B′A′交AB于点D,则S△BA′D=$\frac{1}{5}$. 分析 先利用勾股定理计算出AB=$\sqrt{5}$,再根据旋转的性质得CE=CA=1,A′B′=AB=$\sqrt{5}$,CB′=BC=2,∠B=∠B′,∠A′DB′=∠ACB=90°,则BA′=BC-CA′=1,利用三角形内角和易得∠BDA′=A′CB′=90°,同时可判断Rt△BDA′∽Rt△B′CA′,利用相似比可计算BD=$\frac{2}{5}$$\sqrt{5}$,DA′=$\frac{2}{5}$$\sqrt{5}$,然后根据三角形面积公式求解.
解答 解:∵∠ACB=90°,AC=1,BC=2,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{5}$,
∵△ABC绕顶点C旋转,点A转到BC边上的点A′处,点B转到点F处,
∴CA′=CA=1,A′B′=AB=$\sqrt{5}$,CB′=BC=2,∠B=∠B′,∠A′DB′=∠ACB=90°,
∴BA′=BC-CA′=1,
∵∠CA′B′=∠BA′D,
∴∠BDA′=∠A′CB′=90°,
∴Rt△BDA′∽Rt△B′CA′,
∴$\frac{BD}{CB′}$=$\frac{BA′}{A′B′}$=$\frac{DA′}{CA′}$,即$\frac{BD}{2}$=$\frac{1}{\sqrt{5}}$=$\frac{DA′}{1}$,解得BD=$\frac{2}{5}$$\sqrt{5}$,DA′=$\frac{2}{5}$$\sqrt{5}$,
∴S△BA′D=$\frac{1}{2}$•DA′•BD=$\frac{1}{2}$×$\frac{2}{5}$$\sqrt{5}$×$\frac{\sqrt{5}}{5}$=$\frac{1}{5}$.
故答案为:$\frac{1}{5}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了相似三角形的判定与性质.


科目:初中数学 来源: 题型:选择题
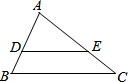 如图,在△ABC中,DE∥BC,$\frac{EC}{AE}$=$\frac{1}{2}$,△ADE的面积为8,则四边形DBCE的面积为( )
如图,在△ABC中,DE∥BC,$\frac{EC}{AE}$=$\frac{1}{2}$,△ADE的面积为8,则四边形DBCE的面积为( )| A. | 10 | B. | 4 | C. | 42 | D. | 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 32006 | B. | 32005 | C. | 32006-1 | D. | 32005-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com