
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
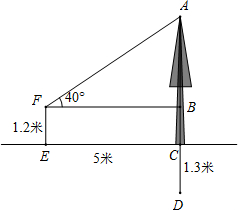 (2012•梧州)如图,某校为搞好新校区的绿化,需要移植树木.该校九年级数学兴趣小组对某棵树木进行测量,此树木在移植时需要留出根部(即CD)1.3米.他们在距离树木5米的E点观测(即CE=5米),测量仪的高度EF=1.2米,测得树顶A的仰角∠BFA=40°,求此树的整体高度AD.(精确到0.1米)(参考数据:sin40°=0.6428,cos40°=0.7660,tan40°=0.8391)
(2012•梧州)如图,某校为搞好新校区的绿化,需要移植树木.该校九年级数学兴趣小组对某棵树木进行测量,此树木在移植时需要留出根部(即CD)1.3米.他们在距离树木5米的E点观测(即CE=5米),测量仪的高度EF=1.2米,测得树顶A的仰角∠BFA=40°,求此树的整体高度AD.(精确到0.1米)(参考数据:sin40°=0.6428,cos40°=0.7660,tan40°=0.8391)查看答案和解析>>
科目:初中数学 来源: 题型:
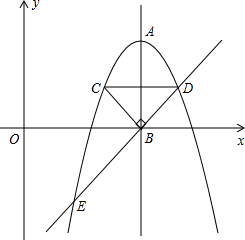 (2012•梧州)如图,抛物线y=-x2+12x-30的顶点为A,对称轴AB与x轴交于点B.在x上方的抛物线上有C、D两点,它们关于AB对称,并且C点在对称轴的左侧,CB⊥DB.
(2012•梧州)如图,抛物线y=-x2+12x-30的顶点为A,对称轴AB与x轴交于点B.在x上方的抛物线上有C、D两点,它们关于AB对称,并且C点在对称轴的左侧,CB⊥DB.| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com